题目内容
3．已知函数f（x）=x2+ax-4在区间（0，1）内只有一个零点，则a的取值范围是（ ）| A． | （-∞，3） | B． | （3，+∞） | C． | （-∞，4） | D． | （4，+∞） |
分析 由△=a2+16＞0及在（0，1）上只有一个零点可知f（0）•f（1）＜0．
解答 解：∵△=a2+16＞0，∴f（x）=0有两个不相等的实数解，且x2+ax-4=0的两根之积为-4＜0，
又f（x）=x2+ax-4在区间（0，1）内只有一个零点，
∴f（0）•f（1）＜0，即-4（x-3）＜0，解得x＞3．
故选：B．
点评 本题考查了二次函数零点与性质，属于基础题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
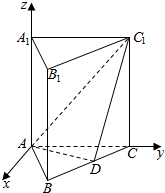已知正三棱柱ABC-A1B1C1的各棱长均为1，D是BC上一点，AD⊥C1D，以A为坐标原点，平面ABC内AC的垂线，AC，AA1所在直线分别为x轴、y轴、z轴，建立如图所示的空间直角坐标系，则点D的坐标为（$\frac{\sqrt{3}}{4}$，$\frac{3}{4}$，0），平面ADC1的一个法向量为（$\sqrt{3}$，-1，1）．