题目内容
9.已知抛物线方程为y2=2p(x+1)(p>0),直线l:x+y=m过抛物线的焦点F且被抛物线截得的弦长为3,则p=$\frac{3}{4}$.分析 由于直线l:x+y=m过抛物线的焦点,得到直线l的方程,再将l的方程代入抛物线方程y2=2p(x+1)(p>0),消去x,得y2+2py-p2-2p=0,设A(x1,y1),B(x2,y2),由根与系数的关系得y1+y2,y1y2;再由弦长公式|AB|=x1+x2+p,可求得|AB|=4p=3,从而求得p的值.
解答 解:由直线l过抛物线的焦点F($\frac{p}{2}$,0),得直线l的方程为x+y=$\frac{p}{2}$.
代入抛物线方程为y2=2p(x+1)(p>0),消去x,得y2+2py-p2-2p=0.
设直线与抛物线交于A(x1,y1),B(x2,y2),
y1+y2=-2p,y1y2=-p2-2p,
∴|AB|=x1+x2+p=2p-(y1+y2)=4p=3,
解得p=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题考查了抛物线的几何性质以及弦长公式的应用,也考查了一定的计算能力,解题时要灵活运用公式,正确解答.

练习册系列答案
相关题目
2.设F1、F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两个焦点,P在双曲线上,若$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|=2ac(c=$\sqrt{{a}^{2}+{b}^{2}}$),则双曲线的离心率为( )
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | 2 | D. | $\frac{\sqrt{5}+1}{2}$ |
3.已知函数f(x)=x2+ax-4在区间(0,1)内只有一个零点,则a的取值范围是( )
| A. | (-∞,3) | B. | (3,+∞) | C. | (-∞,4) | D. | (4,+∞) |
17.过抛物线C:y2=2x的焦点F,且斜率为k(k>0)的直线l交C于R,S两点,若$\overrightarrow{RF}$=2$\overrightarrow{FS}$,则k的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | 2$\sqrt{2}$ |

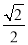 B.
B.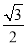
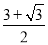 D.
D.