题目内容
9.已知m>0,n>0,向量$\overrightarrow{a}$=(m,1,-3)与$\overrightarrow{b}$=(1,n,2)垂直,则mn的最大值为9.分析 由已知得$\overrightarrow{a}•\overrightarrow{b}$=m+n-6=0,从而m+n=6,由此利用均值定理能求出mn的最大值.
解答 解:∵m>0,n>0,向量$\overrightarrow{a}$=(m,1,-3)与$\overrightarrow{b}$=(1,n,2)垂直,
∴$\overrightarrow{a}•\overrightarrow{b}$=m+n-6=0,即m+n=6,
∴mn≤($\frac{m+n}{2}$)2=9,
当且仅当m=n=3时,取等号,
∴mn的最大值为9.
故答案为:9.
点评 本题考查两数积的最大值的求法,是基础题,解题时要认真审题,注意向量垂直的性质和均值定理的合理运用.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
19.函数f(x)=$\left\{\begin{array}{l}{{3}^{x-2}(x<2)}\\{lo{g}_{3}({x}^{2}-1)(x≥2)}\end{array}\right.$,若f(a)=1,则a的值是( )
| A. | 2 | B. | 1 | C. | 1或2 | D. | 1或-2 |
20.过点C(2,-1)且与直线x+y-3=0垂直的直线是( )
| A. | x+y-1=0 | B. | x+y+1=0 | C. | x-y-3=0 | D. | x-y-1=0 |
17.某四棱锥的三视图如图所示,则该四棱锥的体积是( )


| A. | 36 | B. | 24 | C. | 12 | D. | 6 |
4.在公差为d的等差数列{an}中,“d>1”是“{an}是递增数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.已知命题p:直线$x+2y-\sqrt{2}=0$与直线$x+2y-6\sqrt{2}=0$之间的距离不大于1,命题q:椭圆2x2+27y2=54与双曲线9x2-16y2=144有相同的焦点,则下列命题为真命题的是( )
| A. | p∧(¬q) | B. | (¬p)∧q | C. | (¬p)∧(¬q) | D. | p∧q |
19.已知函数f(x)的图象如图所示,则该函数的定义域、值域分别是( )
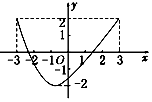

| A. | (-3,3),(-2,2) | B. | [-2,2],[-3,3] | C. | [-3,3],[-2,2] | D. | (-2,2),(-3,3) |