题目内容
已知直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x的四个交点从上到下依次为A,B,C,D四点,则|AB|+|CD|= .
考点:圆与圆锥曲线的综合,直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:求出圆的圆心与半径,抛物线y2=8x的焦点,判断直线y=x-2圆心与焦点的关系,化简|AB|+|CD|=|AD|-2,联立直线与抛物线方程
,利用抛物线的性质,能够推导出|AB|+|CD|的值.
|
解答:
解:由已知圆的方程x2+y2-4x+3=0化为(x-2)2+y2=1,圆的圆心(2,0),半径为1,
抛物线y2=8x的焦点为(2,0),
直线y=x-2过(2,0)点,
则|AB|+|CD|=|AD|-2,
因为
,
可得x2-12x+4=0,
设A(x1,y1),D(x2,y2),
则x1+x2=12,
则有|AD|=(x1+x2)+4=16,
故|AB|+|CD|=16-2=14,
故答案为:14.
抛物线y2=8x的焦点为(2,0),
直线y=x-2过(2,0)点,
则|AB|+|CD|=|AD|-2,
因为
|
可得x2-12x+4=0,
设A(x1,y1),D(x2,y2),
则x1+x2=12,
则有|AD|=(x1+x2)+4=16,
故|AB|+|CD|=16-2=14,
故答案为:14.
点评:本题考查圆锥曲线和直线以及圆的综合运用,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
已知集合M={a,c},N={a,b,c},则M∩N=( )
| A、{a} |
| B、{a,b} |
| C、{a,c} |
| D、{a,b,c} |
若方程
+
=1表示双曲线,则实数k的取值范围是( )
| x2 |
| 1+k |
| y2 |
| 1-k |
| A、k<-1 |
| B、k>1 |
| C、-1<k<1 |
| D、k<-1或k>1 |
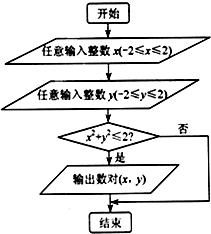 执行如图的程序框图,任意输入一次x(x∈Z,-2≤x≤2)与y(y∈Z,-2≤y≤2),则能输出数对(x,y)的概率为( )
执行如图的程序框图,任意输入一次x(x∈Z,-2≤x≤2)与y(y∈Z,-2≤y≤2),则能输出数对(x,y)的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知命题p:?x∈(0,+∞),log2x<log3x.命题q:?x∈R,x3=1-x2.则下列命题中为真命题的是( )
| A、p∧q | B、¬p∧q |
| C、p∧¬q | D、¬p∧¬q |