题目内容

已知a，b∈R，求证：a4+b4+1≥2ab（2-3ab）
考点：不等式的证明
专题：证明题,作差法
分析：利用作差法，再进行配方，即可证得结论．
解答： 证明：∵a，b∈R，
∴a4+b4+1-2ab（2-3ab）=a4+b4+2a2b2+4a2b2-4ab+1
=（a2+b2）2+（2ab-1）2≥0，
∴a4+b4+1≥2ab（2-3ab）．
点评：本题考查不等式的证明，考查作差法证明不等式，属于基础题．
练习册系列答案
相关题目
已知向量
m
=（sinx，cosx），
n
=(
3
2
，
3
2
)，x∈R，函数f（x）=
m•
n
．
（Ⅰ）求f（x）的最大值；
（Ⅱ）在△ABC中，设角A，B的对边分别为a，b，若B=2A，且b=2af（A-
π
6
），求角C的大小．
设△ABC的内角A，B，C所对的边分别为a，b，c，且有
tanA+tanC
3
=
sinB
cosC
．
（1）求cosA的值；
（2）若b=2，c=3，D为BC上一点．且
CD
=2
DB
，求AD的长．
如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．
（1）若PA=PD，求证：平面PQB⊥平面PAD；
（2）设点M在线段PC上，
PM
MC
=
1
2
，求证：PA∥平面MQB；
（3）在（2）的条件下，若平面PAD⊥平面ABCD，且PA=PD=AD=2，求二面角M-BQ-C的大小．
设f（x）=x2-2x+2m，当x∈[-1，+∞）时，f（x）≥m恒成立，求m的取值范围．
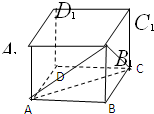已知正方体ABCD-A1B1C1D1的棱长是a，求三棱锥B-AB1C的高．
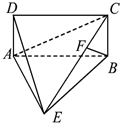如图，四棱锥E-ABCD中，ABCD是矩形，平面EAB⊥平面ABCD，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE．
（1）求证：AE⊥BE；
（2）求二面角A-CD-E的余弦值．
设0＜β＜α＜
π
2
，且cosα=
1
7
 ，  cos(α-β)=
13
14
，则tanβ的值为
 
．
设平面向量
a
，
b
满足| 
a
-3
b
 |≤ 
2
，则
a
•
b
的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网