题目内容
8.已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合,曲线C的极坐标方程为:ρsin2θ=4cosθ,曲线D的参数方程为$\left\{\begin{array}{l}{x=t+2}\\{y=2t-5}\end{array}\right.$(t为参数)(1)将曲线C的极坐标方程化为直角坐标方程,将曲线D的参数方程化为普通方程;
(2)设曲线C与曲线D交于A,B,求向量$\overrightarrow{OA}$•$\overrightarrow{OB}$..
分析 (1)曲线C的极坐标方程为:ρsin2θ=4cosθ,即ρ2sin2θ=4ρcosθ,利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可化为直角坐标方程.曲线D的参数方程为$\left\{\begin{array}{l}{x=t+2}\\{y=2t-5}\end{array}\right.$(t为参数),消去t即可化为直角坐标方程.
(2)设A(x1,y1),B(x2,y2).联立$\left\{\begin{array}{l}{2x-y=9}\\{{y}^{2}=4x}\end{array}\right.$,化为:y2-2y-18=0,利用根与系数的关系及其数量积运算性质即可得出$\overrightarrow{OA}$•$\overrightarrow{OB}$.
解答 解:(1)曲线C的极坐标方程为:ρsin2θ=4cosθ,即ρ2sin2θ=4ρcosθ,化为y2=4x.
曲线D的参数方程为$\left\{\begin{array}{l}{x=t+2}\\{y=2t-5}\end{array}\right.$(t为参数),化为2x-y=9.
(2)设A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{2x-y=9}\\{{y}^{2}=4x}\end{array}\right.$,化为:y2-2y-18=0,
∴y1+y2=2,y1y2=-18.
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=$\frac{1}{16}({y}_{1}{y}_{2})^{2}$+y1y2=$\frac{1}{16}×1{8}^{2}-18$=$\frac{9}{4}$.
点评 本题考查了极坐标方程转化为直角坐标方程、直线与抛物线相切交问题、数量积运算性质,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{\sqrt{7}}{3}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{2}{5}\sqrt{7}$ | D. | $\sqrt{7}$ |
| A. | -1 | B. | 0 | C. | $\frac{1}{4}$ | D. | 4 |
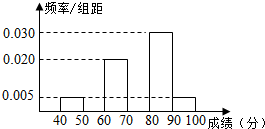 某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),已知成绩在[50,60 )的学生有9人,
某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),已知成绩在[50,60 )的学生有9人,