题目内容
6.已知向量$\overrightarrow{a}$=(cosθ,sinθ),$\overrightarrow{b}$=(2,-1)(1)若$\overrightarrow{a}$⊥$\overrightarrow{b}$,求$\frac{sinθ-cosθ}{sinθ+cosθ}$的值;
(2)若|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,θ∈(0,$\frac{π}{2}$)求tan2θ的值.
分析 (1)利用两个向量垂直的性质,同角三角函数的基本关系,求得tanθ的值,可得要求式子的值.
(2)由条件求得tanθ的值,再利用二倍角的正切公式,求得tan2θ的值.
解答 解:(1)∵向量$\overrightarrow{a}$=(cosθ,sinθ),$\overrightarrow{b}$=(2,-1),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$\overrightarrow{a}•\overrightarrow{b}$=2cosθ-sinθ=0,求得tanθ=2,
∴$\frac{sinθ-cosθ}{sinθ+cosθ}$=$\frac{tanθ-1}{tanθ+1}$=$\frac{1}{3}$.
(2)∵$\overrightarrow{a}$-$\overrightarrow{b}$=(cosθ-2 sinθ+1),|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{(cosθ-2)}^{2}{+(sinθ+1)}^{2}}$=$\sqrt{6+2sinθ-4cosθ}$=2,
∴2sinθ-4cosθ=-2,∴4sin2θ+16cos2θ-16sinθcosθ=4,又θ∈(0,$\frac{π}{2}$),
∴cosθ>0,∴tanθ=$\frac{3}{4}$,tan2θ=$\frac{2tanθ}{1{-tan}^{2}θ}$=$\frac{\frac{3}{2}}{1-\frac{9}{16}}$=$\frac{24}{7}$.
点评 本题主要考查两个向量垂直的性质,同角三角函数的基本关系,二倍角的正切公式,属于基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
16.下列函数中,同时满足①在(0,$\frac{π}{2}$)上是增函数,②为偶函数,③以π为最小正周期的函数是( )
| A. | f(x)=tanx | B. | f(x)=cos2x | C. | f(x)=|sin2x| | D. | f(x)=|sinx| |
15.已知复数z=$\frac{5i}{2+i}$-3i,则|z|等于( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
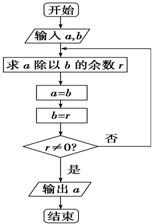 我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=18.
我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=18.