题目内容
1．在平面直角坐标系xOy中，已知直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{2\sqrt{5}}{5}t}\\{y=1+\frac{\sqrt{5}}{5}t}\end{array}\right.$（l为参数），直线l与抛物线y2=4x相交于A，B两点．则线段AB的长为4$\sqrt{10}$．分析 将直线参数方程代入抛物线方程，求出参数的两根之和与两根之积，根据参数的几何意义求出|AB|．
解答 解：将直线l的参数方程代入抛物线方程得1+$\frac{2\sqrt{5}}{5}t$+$\frac{1}{5}{t}^{2}$=$\frac{8\sqrt{5}}{5}t$，
即t2-6$\sqrt{5}$t+5=0，∴t1+t2=6$\sqrt{5}$，t1t2=5．
∴|AB|=|t1-t2|=$\sqrt{（{t}_{1}+{t}_{2}）^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{160}$=4$\sqrt{10}$．
故答案为：4$\sqrt{10}$．
点评 本题考查了直线参数方程的几何意义，属于中档题．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
12．执行如图所示的程序框图，如果输入的x、y∈R，那么输出的S的最大值为（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
9．
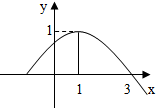函数y=sin（ωx+φ）（x∈R，ω＞0，0≤φ≤2π）的部分图象如图所示，则（ ）
函数y=sin（ωx+φ）（x∈R，ω＞0，0≤φ≤2π）的部分图象如图所示，则（ ）| A． | ω=$\frac{π}{2}$，φ=$\frac{π}{4}$ | B． | ω=$\frac{π}{3}$，φ=$\frac{π}{6}$ | C． | ω=$\frac{π}{4}$，φ=$\frac{π}{4}$ | D． | ω=$\frac{π}{4}$，φ=$\frac{5π}{4}$ |
16．对于参数方程为$\left\{\begin{array}{l}{x=1-tcos30°}\\{y=2+tsin30°}\end{array}\right.$和$\left\{\begin{array}{l}{x=1+tcos30°}\\{y=2-tsin30°}\end{array}\right.$的曲线，正确的结论是（ ）
| A． | 是倾斜角为30°的平行线 | B． | 是倾斜角为30°的同一直线 | ||
| C． | 是倾斜角为150°的同一直线 | D． | 是过点（1，2）的相交直线 |