题目内容
13．化简：$\frac{a-b}{\sqrt{a}+\sqrt{b}}$+$\frac{（\sqrt{a}）^{3}+（\sqrt{b}）^{3}}{a-\sqrt{ab}+b}$=2$\sqrt{a}$．分析 利用根式与分数指数幂互化公式、性质、运算法则、平方差公式、立方差公式求解．
解答 解：$\frac{a-b}{\sqrt{a}+\sqrt{b}}$+$\frac{（\sqrt{a}）^{3}+（\sqrt{b}）^{3}}{a-\sqrt{ab}+b}$
=$\sqrt{a}-\sqrt{b}$+$\sqrt{a}+\sqrt{b}$
=2$\sqrt{a}$．
故答案为：2$\sqrt{a}$．
点评 本题考查有理数指数幂化简求值，是基础题，解题时要注意根式与分数指数幂互化公式、性质、运算法则、平方差公式、立方差公式的合理运用．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
3．与向量$\overrightarrow{a}$=（2，3，6）共线的单位向量是（ ）
| A． | （$\frac{2}{7}$，$\frac{3}{7}$，$\frac{6}{7}$） | B． | （-$\frac{2}{7}$，-$\frac{3}{7}$，-$\frac{6}{7}$） | ||
| C． | （$\frac{2}{7}$，-$\frac{3}{7}$，-$\frac{6}{7}$）和（-$\frac{2}{7}$，$\frac{3}{7}$，$\frac{6}{7}$） | D． | （$\frac{2}{7}$，$\frac{3}{7}$，$\frac{6}{7}$）和（-$\frac{2}{7}$，-$\frac{3}{7}$，-$\frac{6}{7}$） |
1．
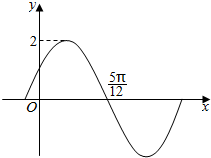已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，且f（0）=f（$\frac{π}{3}$），则（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，且f（0）=f（$\frac{π}{3}$），则（ ）| A． | f（x）的最小正周期为2π | B． | f（x）的图象关于直线x=$\frac{5π}{6}$对称 | ||
| C． | f（$\frac{2π}{3}$）=-2 | D． | f（x）在[0，$\frac{π}{4}$]上是增函数 |
如图所示的四面体OABC中，OA=OB=OC=a，∠AOB=90°，∠BOC=∠AOC=60°，点M，N分别是AB，OC的中点，点S是MN上靠近点N的三等分点．
5．下列函数中，值域为[1，+∞）的是（ ）
| A． | y=2x+1 | B． | y=$\sqrt{x-1}$ | C． | y=$\frac{1}{|x|}$+1 | D． | y=x+$\sqrt{x-1}$ |
2．已知log0.3（m+1）＜log0.3（2m-1），则m的取值范围是（ ）
| A． | （-∞，2） | B． | $（{\frac{1}{2}，2}）$ | C． | （2，+∞） | D． | （-1，2） |