题目内容
11．
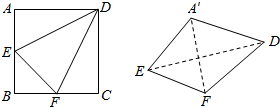如图，边长为2的正方形ABCD中，点E、F分别 是AB、BC的中点，将△ADE，△EBF，△FCD分别沿DE，EF，FD折起，使得A、B、C三点重合于点A′，若四面体A′EFD的四个顶点在同一个球面上，则该球的表面积为（ ）| A． | 8π | B． | 6π | C． | 11π | D． | 5π |
分析 把棱锥扩展为正四棱柱，求出正四棱柱的外接球的半径就是三棱锥的外接球的半径，从而可求球的表面积．
解答 解：由题意可知△A′EF是等腰直角三角形，且A′D⊥平面A′EF．
三棱锥的底面A′EF扩展为边长为1的正方形，
然后扩展为正四棱柱，三棱锥的外接球与正四棱柱的外接球是同一个球，
正四棱柱的对角线的长度就是外接球的直径，直径为：$\sqrt{1+1+4}$=$\sqrt{6}$．
∴球的半径为$\frac{\sqrt{6}}{2}$，
∴球的表面积为$4π•（\frac{\sqrt{6}}{2}）^{2}$=6π．
故选：B．
点评 本题考查几何体的折叠问题，几何体的外接球的半径的求法，考查球的表面积，考查空间想象能力．
练习册系列答案
名师点拨卷系列答案
相关题目
1．
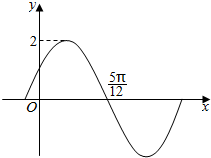已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，且f（0）=f（$\frac{π}{3}$），则（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，且f（0）=f（$\frac{π}{3}$），则（ ）| A． | f（x）的最小正周期为2π | B． | f（x）的图象关于直线x=$\frac{5π}{6}$对称 | ||
| C． | f（$\frac{2π}{3}$）=-2 | D． | f（x）在[0，$\frac{π}{4}$]上是增函数 |
2．已知log0.3（m+1）＜log0.3（2m-1），则m的取值范围是（ ）
| A． | （-∞，2） | B． | $（{\frac{1}{2}，2}）$ | C． | （2，+∞） | D． | （-1，2） |
19．现用系统抽样方法从已编号（1-60）的60枚新型导弹中，随机抽取6枚进行试验，则所选取的6枚导弹的编号可能是（ ）
| A． | 5，10，15，20，25，30 | B． | 2，4，8，16，32，48 | ||
| C． | 5，15，25，35，45，55 | D． | 1，12，34，47，51，60 |
16．设点A，B的坐标分别是（-5，0），（5，0），直线AM，BM相交于点M，且它们的斜率之积是-$\frac{4}{9}$，点M的轨迹方程为（ ）
| A． | $\frac{{x}^{2}}{25}$+$\frac{9{y}^{2}}{100}$=1（x≠±5） | B． | $\frac{{x}^{2}}{25}$-$\frac{9{y}^{2}}{100}$=1（x≠±5） | ||
| C． | $\frac{{y}^{2}}{25}$+$\frac{9{x}^{2}}{100}$=1（y≠±5） | D． | $\frac{{y}^{2}}{25}$-$\frac{9{x}^{2}}{100}$（y≠±5） |
1．已知抛物线x2=4y上的一点P到此抛物线的焦点的距离为2，则点P的纵坐标是（ ）
| A． | 0 | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |