题目内容
13.已知a,b均为正数,$\frac{1}{a}+\frac{4}{b}=1$,求使a+b≥c恒成立的c的取值范围.分析 先用“贴1法”求得a+b的最小值,即a+b=(a+b)•1=(a+b)•($\frac{1}{a}$+$\frac{4}{b}$),展开再用基本不等式求最值即可.
解答 解:因为a,b均为正数,且$\frac{1}{a}+\frac{4}{b}=1$,所以,
a+b=(a+b)•1=(a+b)•($\frac{1}{a}$+$\frac{4}{b}$)
=5+$\frac{b}{a}$+$\frac{4a}{b}$≥5+2$\sqrt{\frac{b}{a}•\frac{4a}{b}}$=9,
即a+b≥9,
根据题意,c≤(a+b)min,∴c≤9.
故实数c的取值范围为:(-∞,9].
点评 本题主要考查了基本不等式在求最值中的应用,其中灵活运用“贴1法”是解决本题的关键,属于基础题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
8.若一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( ) 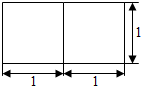

| A. | $\frac{16}{3}$ π | B. | $\frac{19}{3}$ π | C. | $\frac{19}{12}$ π | D. | $\frac{4}{3}$ π |
5.函数$f(x)=\frac{1}{x}ln(\sqrt{6-x-{x^2}}+\sqrt{{x^2}-2x})$的定义域为( )
| A. | [-3,0] | B. | [-3,0) | C. | [-3,0)∪{2} | D. | [-3,0]∪{2} |
2.设集合A={(x,y)|x+y=1},B={(x,y)|2x-y=-4},则A∩B=( )
| A. | {x=-1,y=2} | B. | (-1,2) | C. | {-1,2} | D. | {(-1,2)} |
3.已知甲圆锥的半径是乙圆锥半径的3倍,它的高只有乙圆锥高的$\frac{1}{3}$,则甲圆锥与乙圆锥的体积之比为( )
| A. | 1:1 | B. | 3:1 | C. | 9:1 | D. | 1:9 |