题目内容
3.已知α∈(0,π),且tan($α+\frac{π}{4}$)=$\frac{1}{7}$,则cosα=-$\frac{4}{5}$.分析 由条件利用两角和的正切公式求得tanα的值、再利用同角三角函数的基本关系求得cosα的值.
解答 解:∵α∈(0,π),且tan($α+\frac{π}{4}$)=$\frac{1+tanα}{1-tanα}$=$\frac{1}{7}$,∴tanα=-$\frac{3}{4}$=$\frac{sinα}{cosα}$,
再根据sin2α+cos2α=1,cosα<0,求得cosα=-$\frac{4}{5}$.
点评 本题主要考查两角和的正切公式、同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
11.已知函数f(x)=$\left\{\begin{array}{l}{3x+1,x≤0}\\{|{x}^{2}-4x+1|.x>0}\end{array}\right.$,若函数g(x)=f2(x)-axf(x)恰有6个零点,则a的取值范围是( )
| A. | (0,3) | B. | (1,3) | C. | (2,3) | D. | (0,2) |
15.方程$(2x-y+2)\sqrt{{x^2}+{y^2}-1}=0$表示的曲线是( )
| A. | 一个点与一条直线 | B. | 两个点或一条直线或一个圆 | ||
| C. | 两个点 | D. | 两条射线和一个圆 |
12.正方体ABCD-A1B1C1D1中,E是棱BB1中点,G是DD1中点,F是BC上一点且FB=$\frac{1}{4}$BC,则GB与EF所成的角为( )
| A. | 30° | B. | 120° | C. | 60° | D. | 90° |
 ,集合
,集合 ,则
,则 为( )
为( ) B.
B. C.
C. D.
D.
 的终边经过点
的终边经过点 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.0
D.0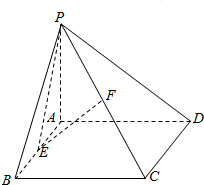 如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点
如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点