题目内容
3.已知函数f(x)=ax,g(x)=logax(a>0,a≠1),若$f({\frac{1}{2}})•g({\frac{1}{2}})<0$,那么f(x)与g(x)在同一坐标系内的图象可能是下图中的( )| A. | 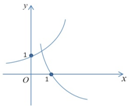 | B. | 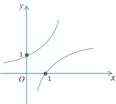 | C. | 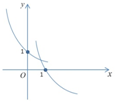 | D. | 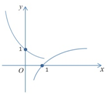 |
分析 判断得出f(x)>0,利用不等式得出g($\frac{1}{2}$)<0,判断出a>1,根据指数,对数函数的单调性得出答案.
解答 解:∵函数f(x)=ax,g(x)=logax(a>0,a≠1),
∴f(x)>0,
∵$f({\frac{1}{2}})•g({\frac{1}{2}})<0$,
∴g($\frac{1}{2}$)<0,
∴a>1,
根据指数,对数函数的单调性得出:f(x),g(x)都为增函数.
故选:B
点评 本题简单的考查了指数,对数函数的图象性质,属于容易题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
8.一个多面体的三视图如图所示,则此多面体的表面积是( )


| A. | 10 | B. | 12 | C. | 8+4$\sqrt{2}$ | D. | 12+4$\sqrt{2}$ |
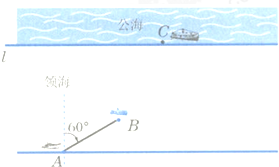 设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题:
设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题: