题目内容
12.如图,已知矩形ABCD中,AB=2,AD=1,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM,连结BM.
(Ⅰ)求证:BM⊥平面ADM;
(Ⅱ)求二面角A-DM-C的余弦值;
(Ⅲ)若点E是线段DB上的一动点,问点E在何位置时,三棱锥M-ADE的体积为$\frac{{\sqrt{2}}}{12}$.
分析 (Ⅰ)推导出AM⊥BM,由此能证明BM⊥平面ADM,
(2)分别取AM,AB的中点O和N,建立空间直角坐标系,利用向量法能求出二面角A-DM-C的余弦值.
(3)求出平面ADM的一个法向量,从而点E到平面ADM的距离d=$\frac{|\overrightarrow{AE}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\sqrt{2}λ$,由此利用体积公式能求出E为BD的中点时,三棱锥M-ADE的体积为$\frac{{\sqrt{2}}}{12}$.
解答 证明:(Ⅰ)∵矩形ABCD中,AB=2,AD=1,M为DC的中点,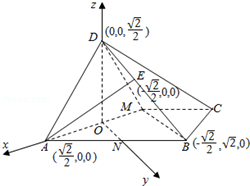
∴AM=BM=$\sqrt{2}$,
∴AM2+BM2=AB2,∴AM⊥BM.
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,
∴BM⊥平面ADM,
解:(2)分别取AM,AB的中点O和N,则ON∥BM,
在(1)中证明BM⊥平面ADM,
∴ON⊥⊥平面ADM,ON⊥AM,ON⊥OD,
∵AD=DM,∴DO⊥AM,
建立空间直角坐标系,如图,
D(0,0,$\frac{\sqrt{2}}{2}$),M(-$\frac{\sqrt{2}}{2}$,0,0),C(-$\sqrt{2}$,$\frac{\sqrt{2}}{2}$,0),
则$\overrightarrow{DM}$=(-$\frac{\sqrt{2}}{2}$,0,-$\frac{\sqrt{2}}{2}$),$\overrightarrow{MC}$=(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$,0),
设$\overrightarrow{m}$=(x,y,z)是平面CDM的法向量,
则$\left\{\begin{array}{l}{\overrightarrow{DM}•\overrightarrow{m}=-\frac{\sqrt{2}}{2}x-\frac{\sqrt{2}}{2}z=0}\\{\overrightarrow{MC}•\overrightarrow{m}=-\frac{\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}y=0}\end{array}\right.$,
令x=1,则y=1,z=-1,即$\overrightarrow{m}$=(1,1,-1),
由题意知$\overrightarrow{n}$=(0,1,0)是平面ADM的法向量,
设二面角A-DM-C的平面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
∴二面角A-DM-C的余弦值为$\frac{\sqrt{3}}{3}$.
(3)D(0,0,$\frac{\sqrt{2}}{2}$),A($\frac{\sqrt{2}}{2}$,0,0),B(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$,0),
∴$\overrightarrow{DB}$=(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$,-$\frac{\sqrt{2}}{2}$),
∵E是线段DB上的一个动点,
∴$\overrightarrow{DE}$=$λ\overrightarrow{DB}$=(-$\frac{\sqrt{2}}{2}λ$,$\sqrt{2}λ$,-$\frac{\sqrt{2}}{2}$λ),则E(-$\frac{\sqrt{2}}{2}$λ,$\sqrt{2}λ$,$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$λ),
∴$\overrightarrow{AE}$=(-$\frac{\sqrt{2}}{2}$λ-$\frac{\sqrt{2}}{2}$,$\sqrt{2}λ$,$\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}$λ),
$\overrightarrow{n}$=(0,1,0)是平面ADM的一个法向量.
点E到平面ADM的距离d=$\frac{|\overrightarrow{AE}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\sqrt{2}λ$,
则VM-ADE=$\frac{1}{3}{S}_{△ADM}•d$=$\frac{1}{3}×\frac{1}{2}×1×1×\sqrt{2}$λ=$\frac{\sqrt{2}}{12}$,
解得λ=$\frac{1}{2}$,则E为BD的中点.
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法中,考查满足条件的点的位置的确定,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
| A. | (-∞,0) | B. | (-∞,0] | C. | (-∞,1) | D. | (-∞,1] |
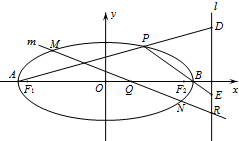 椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=$\frac{2\sqrt{2}}{3}$.
椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=$\frac{2\sqrt{2}}{3}$.