题目内容
13.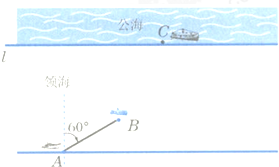 设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题:
设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题:(1)如果走私船和巡逻艇都是沿直线航行,那么走私船能被截获的点是哪些?
(2)根据截获点的轨迹,探讨“可截获区域”和“非截获区域”.
分析 以A为原点,以正东方向为x轴,以海里为单位建立直角坐标系,设|AB|=2t(t>0);
(1)设截获点为P(x,y),利用|PA|=2|PB|得出截获点的轨迹是圆;
(2)设点Q(x,y)在截获点所在的圆内部,列出不等式求出可截获区域和非截获区域.
解答 解:以A为原点,以正东方向为x轴,并以海里为单位建立直角坐标系,
如图所示;
设|AB|=2t,(t>0),则$B=(\sqrt{3}t,t)$;
(1)设截获点为P(x,y),则|PA|=2|PB|,
即$\sqrt{{x^2}+{y^2}}=2\sqrt{(x-\sqrt{3t{)^2}}+{{(y-t)}^2}}$,
化简得${(x-\frac{{4\sqrt{3}}}{3}t)^2}+{(y-\frac{4}{3}t)^2}={(\frac{4}{3}t)^2}$;
所以,截获点的轨迹是以$D(\frac{{4\sqrt{3}}}{3}t,\frac{4}{3}t)$为圆心,$\frac{4}{3}t$为半径的圆;
(2)设点Q(x,y)在圆D内部,则
${(x-\frac{{4\sqrt{3}}}{3}t)^2}+{(y-\frac{4}{3}t)^2}<{(\frac{4}{3}t)^2}$,
化简得$\sqrt{{x^2}+y{\;}^2}>2\sqrt{(x-\sqrt{3t{)^2}}+{{(y-t)}^2}}$,
即|QA|>2|QB|;
所以,可截获区域为领海上的圆D外部,
非截获区域为领海上的圆D内部.
点评 本题考查了圆的方程与方向向量的应用问题,也考查了数学建模的应用问题,是综合性题目

练习册系列答案
相关题目
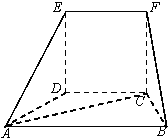 在如图的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.