题目内容
2.直角三角形ABC的三边长分别是a,b,c,且c为斜边的长.(1)若a,b,c成等比数列,且a=2,求c的值;
(2)已知a,b,c均为正整数,若a,b,c是三个连续的整数,求三角形ABC的面积.
分析 (1)根据等比数列的性质,结合勾股定理,即可求出c的值;
(2)根据三边长为三个连续的正整数,利用勾股定理,即可求出三边的长,从而求出三角形的面积.
解答 解:(1)直角△ABC中,三边长a,b,c成等比数列,且a=2,
∴c=$\frac{{b}^{2}}{2}$;
又c2=a2+b2=22+b2,
∴c2=4+2c,
解得c=1+$\sqrt{5}$或c=1-$\sqrt{5}$(不合题意,舍去),
∴c的值为1+$\sqrt{5}$;
(2)直角△ABC中,三边长a,b,c,且c为斜边,
当a,b,c为三个连续的正整数时,
(b-1)2+b2=(b+1)2,
解得b=4或b=0(不合题意,舍去);
∴a=3,c=5,
∴△ABC的面积为S=$\frac{1}{2}$ab=$\frac{1}{2}$×3×4=6.
点评 本题考查了等比数列与等差数列的应用问题,也考查了直角三角形中勾股定理的应用问题,是基础题目.

练习册系列答案
相关题目
12.在空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,0,0),(2,1,1),(0,1,1).若画该四面体三视图时,正视图以zOy平面为投影面,则得到的侧视图是( )
| A. |  | B. | 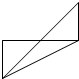 | C. | 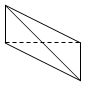 | D. | 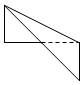 |
17.若实数x,y满足不等式组$\left\{\begin{array}{l}{|x-1|≤1}\\{y≥0}\\{y≤x+1}\end{array}\right.$,则下列结论中正确的是( )
| A. | 2x-y≥0 | B. | 2x-y≤3 | C. | x+y≤6 | D. | x+y<2 |
11.设全集U=R,若集合A={x|y=log2(4-x2)},集合B={y|y=2x-1,x∈R},则集合∁U(A∩B)=( )
| A. | (-1,2) | B. | [-1,2) | C. | (-∞,-1]∪[2,+∞) | D. | (-∞,-1)∪[2,+∞) |