题目内容

14．已知数列{an}中，a3=3，an+1=an+2，则a2+a4=6，an=2n-3．

分析 由数列{an}中，a3=3，an+1=an+2，可得数列{an}是等差数列，公差为2，利用等差数列的通项公式及其性质即可得出．

解答 解：∵数列{an}中，a3=3，an+1=an+2，
∴数列{an}是等差数列，公差为2，
∴an=a3+2（n-3）=3+2（n-3）=2n-6．
∴a2+a4=2a3=6．
故答案分别为：6；2n-3．

点评 本题考查了等差数列的通项公式及其性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
4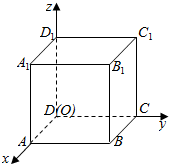．以正方体ABCD-A1B1C1D1的顶点D为坐标原点O，如图建立空间直角坐标系，则与$\overrightarrow{D{B_1}}$共线的向量的坐标可以是（　　）
A．（2，-2，2）B．（-2，-2，2）C．（-2，2，2）D．（-2，-2，-2）
5．用更相减损术法，计算56和264的最大公约数时，需要做的减法次数是（　　）
A．5、B．6C．7D．8
2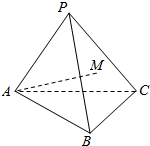．如图，在三棱锥P-ABC中，AB=AC=PB=PC=10，PA=8，BC=12，点M在平面PBC内，且AM=7，设异面直线AM与BC所成角为α，则cosα的最大值为（　　）
A．$\frac{1}{7}$B．$\frac{3}{7}$C．$\frac{6}{7}$D．$\frac{4\sqrt{3}}{7}$
9．若0＜y≤x＜$\frac{π}{2}$且tanx=3tany，则x-y的最大值为$\frac{π}{6}$．
19．设直线l的方向向量是$\overrightarrow{u}$=（-2，2，t），平面α的法向量$\overrightarrow{v}$=（6，-6，12），若直线l⊥平面α，则实数t等于（　　）
A．4B．-4C．2D．-2
6．盒子中有5个大小形状完全相同的小球，其中黑色小球有3个，标号分别为1，2，3，白色小球有2个，标号分别为1，2．
（Ⅰ）若从盒中任取两个小球，求取出的小球颜色相同且标号之和小于或等于4的概率；
（Ⅱ）若盒子里再放入一个标号为4的红色小球，从中任取两个小球，求取出的两个小球颜色不同且标号之和大于3的概率．
3．已知函数f（x）=sin（ωx+φ）对任意的x∈R满足f（x）≤|f（$\frac{π}{4}$）|，若函数g（x）=cos（ωx+φ）-1，则g（$\frac{π}{4}$）的值为（　　）
A．-3B．1C．-1D．1或-3
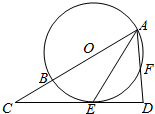4．如图所示，⊙O的圆心O在Rt△ACD的斜边AC上，且⊙O过顶点A，与边CD相切于点E，与边AD、AC分别相交于点F，B．
（1）求证：AE是∠CAD的平分线；
（2）若CE=10，CB=5，求AE的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网