题目内容
16.已知一只蚂蚁在边长分别为5,12,13的三角形的边上随机爬行,则其恰在离三个顶点的距离都大于1的地方的概率为( )| A. | $\frac{π}{60}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{π}{3}$ |
分析 先求出三角形的周长,再求出据“恰在离三个顶点距离都大于1”,线段长为30-6=24,利用几何概型概率公式求出恰在离三个顶点距离都大于1的地方的概率.
解答 解:一只蚂蚁在边长分别为5,12,13的三角形的边上随机爬行,所以周长为30,
而“恰在离三个顶点距离都大于1”,线段长为30-6=24,
所以恰在离三个顶点距离都大于1的地方的概率为$\frac{24}{30}$=$\frac{4}{5}$.
故选:C.
点评 本题主要考查几何概型概率公式、对立事件概率公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知定义在R上的函数f(x)满足f(x)=(x+2),且当-l≤x≤1时,f(x)=2|x|,函数g(x)=x+$\sqrt{2}$,实数a,b满足b>a>3.若?x1∈[a,b],?x2∈[-$\sqrt{2}$,0],使得f(x1)=g(x2)成立,则b-a的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
1.已知sinα-cosα=$\frac{1}{3}$,则cos($\frac{π}{2}$-2α)=( )
| A. | -$\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{8}{9}$ | D. | $\frac{\sqrt{17}}{9}$ |
8.命题“?x∈N,x2>x”的否定为( )
| A. | ?x∈N,x2≤x | B. | ?x0∈N,${x}_{0}^{2}$≤x0 | C. | ?x∉N,x2>x | D. | ?x0∉N,${x}_{0}^{2}$≤x0 |
5.某产品的广告费用x万元与销售额y万元的统计数据如表:
根据上表可得回归方程$\widehaty=9.4x+a$,据此模型预测,广告费用为6万元时的销售额为( )万元.
| 广告费用x | 2 | 3 | 4 | 5 |
| 销售额y | 26 | 39 | 49 | 54 |
| A. | 65.5 | B. | 66.6 | C. | 67.7 | D. | 72 |
14.已知图甲是函数f(x)的图象,图乙是由图甲变换所得,则图乙中的图象对应的函数可能是( )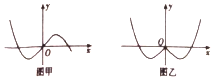
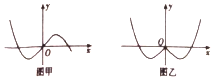
| A. | y=f(|x|) | B. | y=|f(x)| | C. | y=f(-|x|) | D. | y=-f(-|x|) |