题目内容
己知点P(x,y)满足条件
(k为常数),若z=x+3y的最大值为-8,则k= .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:画出可行域,将目标函数变形,画出相应的直线,将其平移,数学结合当直线移至点A时,纵截距最大,z最大,代值可得k的方程,解方程可得.
解答:
解:画出可行域,将z=x+3y变形为y=-
x+
z,
画出直线y=-
x平移至点A时,纵截距最大,z最大,
联立方程得
,解得
代入已知可得z=-
+3(-
)=-8,解得k=6.
故答案为:6

| 1 |
| 3 |
| 1 |
| 3 |
画出直线y=-
| 1 |
| 3 |
联立方程得
|
|
代入已知可得z=-
| k |
| 3 |
| k |
| 3 |
故答案为:6

点评:本题考查简单线性规划,画不等式组的可行域是解决问题的关键,属中档题.

练习册系列答案
相关题目
已知定义在D=[-4,4]上的函数f(x)=
,对任意x∈D,存在x1,x2∈D,使得f(x1)≤f(x)≤f(x2),则|x1-x2|最大与最小值之和为( )
|
| A、7 | B、8 | C、9 | D、10 |
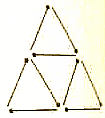 用9根火柴棒搭成的图案如图所示,移动2根火柴棒,使这9根火柴棒搭成一个中心对称图形,并画出这个图形.
用9根火柴棒搭成的图案如图所示,移动2根火柴棒,使这9根火柴棒搭成一个中心对称图形,并画出这个图形.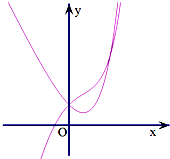 已知函数f(x)=ex-x2的导函数为f′(x),y=f(x)与y=f′(x)在同一直角坐标系下的部分图象如图所示,若方程f′(x)-f(a)=0在x∈(-∞,a]上有两解,则实数a的取值范围是
已知函数f(x)=ex-x2的导函数为f′(x),y=f(x)与y=f′(x)在同一直角坐标系下的部分图象如图所示,若方程f′(x)-f(a)=0在x∈(-∞,a]上有两解,则实数a的取值范围是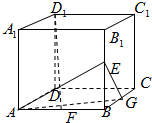 如图正方体ABCD-A1B1C1D1中,E、F、G分别是BB1、AB、BC的中点.
如图正方体ABCD-A1B1C1D1中,E、F、G分别是BB1、AB、BC的中点.