题目内容
3.已知某程序框图如图所示,则执行该程序框图输出的结果是( )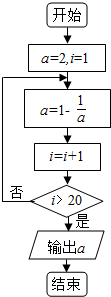
| A. | $\frac{1}{2}$ | B. | -1 | C. | 2 | D. | -2 |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知该程序的作用是利用循环计算变量a的值并输出,依次写出每次循环得到的a,i的值,当i=21时,满足条件,计算即可得解.
解答 解:程序运行过程中,各变量的值如下表示:
a i 是否继续循环
循环前 2 1
第一圈 $\frac{1}{2}$ 2 是
第二圈-1 3 是
第三圈 2 4 是
…
第18圈 2 19 是
第19圈 $\frac{1}{2}$ 20 是
第20圈-1 21 否
故最后输出的a值为-1.
故选:B.
点评 本题主要考查了循环结构,写程序的运行结果,是算法这一模块最重要的题型,属于基础题.

练习册系列答案
相关题目
14.某地区交通执法部门从某日上午9时开始对经过当地的200名车辆驾驶人员驾驶的车辆进行超速测试并分组,并根据测速的数据制作了频率分布图:
(1)求z,y,x的值;
(Ⅱ)若在第2,3,4,5组用分层抽样的方法随机抽取12名驾驶人员做回访调查,并在这12名驾驶人员中任意选3人,这3人中超速在[20%,80%)内的人数记为ξ,求ξ的数学期望.
| 组号 | 超速分组 | 频数 | 频率 | 频率 组距 |
| 1 | [0,20%] | 176 | 0.88 | z |
| 2 | [20%,40%] | 12 | 0.06 | 0.0030 |
| 3 | [40%,60%] | 6 | y | 0.0015 |
| 4 | [60%,80%] | 4 | 0.02 | 0.0010 |
| 5 | [80%,100%] | x | 0.01 | 0.0005 |
(Ⅱ)若在第2,3,4,5组用分层抽样的方法随机抽取12名驾驶人员做回访调查,并在这12名驾驶人员中任意选3人,这3人中超速在[20%,80%)内的人数记为ξ,求ξ的数学期望.
11.已知函数f(x)=x3+bx2+cx+d的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为6x-y+7=0.
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调区间.
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调区间.
8.若复数z=$\frac{{{{(1-i)}^2}}}{1+i}$,则|z|=( )
| A. | 8 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
12.已知函数$f(x)=sin(ωx+φ)(ω>0,0<φ<\frac{π}{2})$的图象经过点$B(-\frac{π}{6},0)$,且f(x)的相邻两个零点的距离为$\frac{π}{2}$,为得到y=f(x)的图象,可将y=sinx图象上所有点( )
| A. | 先向右平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| B. | 先向左平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| C. | 先向左平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变 | |
| D. | 先向右平移$\frac{π}{3}$个单位长度,再将所得点的横坐标变为原来的2倍,纵坐标不变 |