题目内容
15.某架飞机载有5位空降兵空降到A、B、C三个地点,每位空降兵都要空降到A、B、C中任意一个地点,且空降到每一个地点的概率都是$\frac{1}{3}$,用ξ表示地点C空降人数,求:(Ⅰ)地点A空降1人,地点B、C各空降2人的概率;
(Ⅱ)随机变量ξ的分布列与期望.
分析 (I)先求出基本事件的总数,再求出“地点A空降1人,地点B、C各空降2人”包含的基本事件个数,由此能求出所求事件的概率.
( II)由题意知随机变量ξ~B(5,$\frac{1}{3}$),由此能求出随机变量ξ的分布列和数学期望.
解答 解:(I)基本事件的总数为35个,
“地点A空降1人,地点B、C各空降2人”包含的基本事件为$C_5^1C_4^2$,…(3分)
所以所求事件的概率为:$P=\frac{C_5^1C_4^2}{3^5}=\frac{10}{81}$;…(5分)
( II)由题意知随机变量ξ~B(5,$\frac{1}{3}$),…(7分)
∴随机变量ξ的所有可能取值为0,1,2,3,4,5,
P(ξ=0)=${C}_{5}^{0}(\frac{2}{3})^{5}$=$\frac{32}{243}$,
P(ξ=1)=${C}_{5}^{1}•\frac{1}{3}•(\frac{2}{3})^{4}$=$\frac{80}{243}$,
P(ξ=2)=${C}_{5}^{2}(\frac{1}{3})^{2}(\frac{2}{3})^{3}$=$\frac{80}{243}$,
P(ξ=3)=${C}_{5}^{3}(\frac{1}{3})^{3}(\frac{2}{3})^{2}$=$\frac{40}{243}$,
P(ξ=4)=${C}_{5}^{4}(\frac{1}{3})^{4}•\frac{2}{3}$=$\frac{10}{243}$,
P(ξ=5)=${C}_{5}^{5}(\frac{1}{3})^{5}$=$\frac{1}{243}$,…(10分)
所以随机变量ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{32}{243}$ | $\frac{80}{243}$ | $\frac{80}{243}$ | $\frac{40}{243}$ | $\frac{10}{243}$ | $\frac{1}{243}$ |
根据二项分布得数学期望$Eξ=5×\frac{1}{3}=\frac{5}{3}$.…(12分)
点评 本题考查概率的求法,考查离散型承受机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

| A. | {x|-1≤x≤0} | B. | {x|0<x<2} | C. | {x|-1<x<0} | D. | {x|-1<x≤0} |
| A. | $\frac{ab+bc+ac}{{a}^{2}+{b}^{2}+{c}^{2}}$ | B. | -$\frac{ab+bc+ac}{{a}^{2}+{b}^{2}+{c}^{2}}$ | ||
| C. | $\frac{2ab}{{a}^{2}+{b}^{2}}$ | D. | -$\frac{2ab}{{a}^{2}+{b}^{2}}$ |
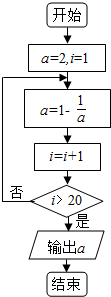
| A. | $\frac{1}{2}$ | B. | -1 | C. | 2 | D. | -2 |
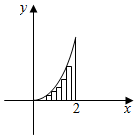 先阅读参考材料,再解决此问题:
先阅读参考材料,再解决此问题: