题目内容

13．若（5x+4）10=a10x10+a9x9+…+a1x+a0，求a0-a1+a2-a3+…-a9+a10的值．

分析 由题意，令x=-1，可得要求式子的值．

解答 解：∵（5x+4）10=a10x10+a9x9+…+a1x+a0，
∴令x=-1，可得 a0-a1+a2-a3+…-a9+a10 =（-5+4）10=1．

点评 本题主要考查二项式定理的应用，注意根据题意，分析所给代数式的特点，通过给二项式的x赋值，求展开式的系数和，可以简便的求出答案，属于基础题．

练习册系列答案
相关题目
3．已知某程序框图如图所示，则执行该程序框图输出的结果是（　　）
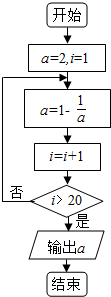
A．$\frac{1}{2}$B．-1C．2D．-2
4．对任意正整数n，设an是方程x3+$\frac{x}{n}$=1的实数根．求证：
（1）an+1＞an；
（2）$\sum_{i=1}^{n}$$\frac{1}{（i+1）^{2}{a}_{i}}$＜an．
1．数列{an}满足a1=2，an+1=$\frac{{2}^{n+1}{a}_{n}}{（n+\frac{1}{2}）{a}_{n}+{2}^{n}}$（n∈N*）
（Ⅰ）设bn=$\frac{{2}^{n}}{{a}_{n}}$，求数列{an}，{bn}的通项公式；
（Ⅱ）设cn=$\frac{1}{{b}_{n+1}-1}$，数列{cn}的前n项和为Sn，不等式$\frac{1}{4}$m2-$\frac{1}{4}$m＞Sn，对一切n∈N*成立，求实数m的范围．
8．某种机器在一个工作班的8小时内，需要工作人员操控累计2个小时才能正常运行，当机器需用操控而无人操控时，机器自动暂停运行．每台机器在某一时刻是否用人操控彼此之间相互独立．
（1）若在一个工作班内有4台相同机器，求在同一时刻需用人操控的平均台数．
（2）若要求一人操控的所有机器正常运行的概率控制在不低于0.9的水平，且该人待工而闲的槪率小于0.6．试探讨：一人操控1台、2台、3台机器这三种工作方案中，哪种方案符合要求，并说明理由．
18．在数列{an}中，a1=1，an+1•an=an-an+1
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若bn=lg$\frac{{a}_{n+2}}{{a}_{n}}$，求数列{bn}的前n项和Sn．
5．设数列{an}满足：a1=0，an+1=an+（n+1）3n．
（1）求数列{an}的通项公式；
（2）设bn=$\frac{4{a}_{n}+3}{{4}^{n}}$，求数列{bn}中的最大项的值．
2．在△ABC中，角A，B，C的对边分别为a．b．c，且满足2bsin（C+$\frac{π}{6}$）=a+c．
（I）求角B的大小；
（Ⅱ）若点M为BC中点，且AM=AC，求sin∠BAC．
3．设集合M={x|x≥-3}，N={x|x≤1}，则M∩N=（　　）
A．RB．（-∞，-3]∪[1，+∞）C．[-3，1]D．∅

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网