题目内容
11.求函数y=4cosx+3sinx的最大值和最小值,并指出取得最值时x的值.分析 直接利用两角和与差的三角函数化简函数的表达式,通过余弦函数的值域求解即可.
解答 解:y=4cosx+3sinx=5sin(x+θ),其中tanθ=$\frac{4}{3}$,
所以当x+θ=$\frac{π}{2}$+2kπ,k∈Z时,即x=$\frac{π}{2}$+2kπ-arctan$\frac{4}{3}$,k∈Z时,函数有最大值,最大值为5,
以当x+θ=-$\frac{π}{2}$+2kπ,k∈Z时,x=-$\frac{π}{2}$+2kπ-arctan$\frac{4}{3}$,k∈Z时,函数有最小值,最小值为-5,
点评 本题考查两角和与差的三角函数,三角函数的最值的求法,基本知识的考查.

练习册系列答案
相关题目
6.已知{an}是等差数列,Sn为其前n项和,若正整数i,j,k,l满足i≤k≤l≤j,且i+j=k+l,则( )
| A. | aiaj≤akal | B. | aiaj≥akal | C. | SiSj<SkSl | D. | SiSj≥SkSl |
5.设集合A={x|x2-2x≥0},B={x|-1<x≤2},则(∁RA)∩B=( )
| A. | {x|-1≤x≤0} | B. | {x|0<x<2} | C. | {x|-1<x<0} | D. | {x|-1<x≤0} |
3.已知某程序框图如图所示,则执行该程序框图输出的结果是( )
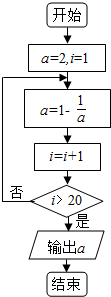

| A. | $\frac{1}{2}$ | B. | -1 | C. | 2 | D. | -2 |