题目内容

8．若复数z=$\frac{{{{（1-i）}^2}}}{1+i}$，则|z|=（　　）
A．8B．2$\sqrt{2}$C．2D．$\sqrt{2}$

分析 直接利用复数的模的运算法则化简求解即可．

解答 解：复数z=$\frac{{{{（1-i）}^2}}}{1+i}$，则|z|=$|\frac{-2i}{1+i}|$=$\frac{2}{\sqrt{1+1}}$=$\sqrt{2}$．
故选：D．

点评 本题考查复数的模的求法，复数的基本运算，是基础题．

练习册系列答案
相关题目
16．若sinα=$\frac{3}{5}$，则
①sin（180°-α）=$\frac{3}{5}$；
②sin（π+α）=-$\frac{3}{5}$；
③sin（-α）=-$\frac{3}{5}$；
④sin（7π-α）=$\frac{3}{5}$；
⑤cos（90°-α）=$\frac{3}{5}$；
⑥cos（$\frac{π}{2}$+α）=-$\frac{3}{5}$；
⑦cos（$\frac{3π}{2}$+α）=$\frac{3}{5}$；
⑧cos（270°-α）=-$\frac{3}{5}$．
19．已知集合A={y|y=2x-1，x∈R}，B={x|x2-x-2＜0}，则（　　）
A．-1∈AB．$\sqrt{3}$∉BC．A∩（∁RB）=AD．A∪B=A
16．设函数f（x）=$\sqrt{a{x^2}+bx+c}$（a，b，c∈R）的定义域和值域分别为A，B，若集合{（x，y）|x∈A，y∈B}对应的平面区域是正方形区域，则实数a，b，c满足（　　）
A．|a|=4B．a=-4且b2+16c＞0C．a＜0且b2+4ac≤0D．以上说法都不对
3．已知某程序框图如图所示，则执行该程序框图输出的结果是（　　）
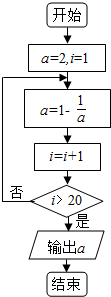
A．$\frac{1}{2}$B．-1C．2D．-2
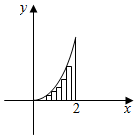13．已知函数f（x）=x2+bx+1满足f（-x）=f（x+1），若存在实数t，使得对任意实数x∈[l，m]，都有f（x+t）≤x成立，则实数m的最大值为3．
20．先阅读参考材料，再解决此问题：
参考材料：求抛物线弧y=x2（0≤x≤2）与x轴及直线x=2围成的封闭图形的面积
解：把区间[0，2]进行n等分，得n-1个分点A（$\frac{2i}{n}$，0）（i=1，2，3，…，n-1），过分点Ai，作x轴的垂线，交抛物线于Bi，并如图构造n-1个矩形，先求出n-1个矩形的面积和Sn-1，再求$\underset{lim}{n→∞}$Sn-1，即是封闭图形的面积，又每个矩形的宽为$\frac{2}{n}$，第i个矩形的高为（$\frac{2i}{n}$）2，所以第i个矩形的面积为$\frac{2}{n}$•（$\frac{2i}{n}$）2；
Sn-1=$\frac{2}{n}$[$\frac{4•{1}^{2}}{{n}^{2}}$+$\frac{4•{2}^{2}}{{n}^{2}}$+$\frac{4•{3}^{2}}{{n}^{2}}$+…+$\frac{4•（n-1）^{2}}{{n}^{2}}$]=$\frac{8}{{n}^{3}}$[12+22+32+…+（n-1）2]=$\frac{8}{{n}^{3}}$•$\frac{n（n-1）（2n-1）}{6}$
所以封闭图形的面积为$\underset{lim}{n→∞}$$\frac{8}{{n}^{3}}$•$\frac{n（n-1）（2n-1）}{6}$=$\frac{8}{3}$
阅读以上材料，并解决此问题：已知对任意大于4的正整数n，不等式$\sqrt{1-\frac{{1}^{2}}{{n}^{2}}}$+$\sqrt{1-\frac{{2}^{2}}{{n}^{2}}}$+$\sqrt{1-\frac{{3}^{2}}{{n}^{2}}}$+…+$\sqrt{1-\frac{（n-1）^{2}}{{n}^{2}}}$＜an恒成立，则实数a的取值范围为[$\frac{π}{4}$，+∞）．
17．已知函数y=sin（x+$\frac{π}{6}$）+sin（x-$\frac{π}{6}$）+2cosx+a的最小值是1，则a的值为$1+\sqrt{7}$．
18．在数列{an}中，a1=1，an+1•an=an-an+1
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若bn=lg$\frac{{a}_{n+2}}{{a}_{n}}$，求数列{bn}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网