题目内容
10.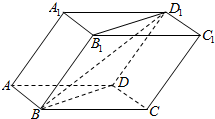 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{\sqrt{39}}{3}$ |
分析 延长AD,过D1作D1E⊥AD于E,连结BE,说明∠D1BE为直线BD1与平面ABCD所成的角,然后求解即可.
解答  解:延长AD,过D1作D1E⊥AD于E,连结BE,
解:延长AD,过D1作D1E⊥AD于E,连结BE,
因为平面A1ADD1⊥平面ABCD,平面A1ADD1∩平面ABCD=AD,
所以D1E⊥平面ABCD,即BE为BD1在平面ABCD内的射影,
所以∠D1BE为直线BD1与平面ABCD所成的角,
因为D1E=2sin60°=$\sqrt{3}$,BE=$\sqrt{{AB}^{2}+{AE}^{2}}$=$\sqrt{13}$,
所以,tan∠D1BE=$\frac{\sqrt{3}}{\sqrt{13}}$=$\frac{\sqrt{39}}{13}$.
故选:C.
点评 本题考查直线与平面所成角的求法,考查计算能力,空间想象能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

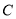 的离心率为
的离心率为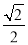 ,
,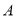 、
、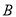 分别为左、右顶点,
分别为左、右顶点,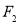 为其右焦点,
为其右焦点,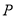 是椭圆
是椭圆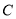 上异于
上异于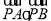 的最小值为-2.
的最小值为-2.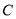 的标准方程;
的标准方程;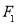 的直线
的直线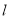 交椭圆
交椭圆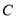 于
于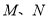 两点,求
两点,求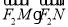 的取值范围.
的取值范围. ,
, ,
, ,若
,若 为实数,
为实数, ,则
,则 ( )
( ) B.
B. C.1 D.2
C.1 D.2