题目内容
7.设向量$\overrightarrow{a}$=(sinx,cosx),$\overrightarrow{b}$=(cosx,$\sqrt{3}$cosx),x∈R,函数f(x)=$\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})$.(1)求函数f(x)的最小正周期;
(2)△ABC中边a、b、c所对的角为A、B、C,若acosB+bcosA=2ccosC,c=$\sqrt{3}$,当f($\frac{B}{2}$)取最大值时,求△ABC的面积.
分析 (1)将f(x)化简成y=Asin(ωx+φ)形式,带入周期公式求出;
(2)利用正弦定理将条件化简得出C,根据f($\frac{B}{2}$)取最大值求出B,然后解三角形.
解答 解:(1)f(x)=$\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})$=$\overrightarrow{a}$2+$\overrightarrow{a}•\overrightarrow{b}$=1+sinxcosx+$\sqrt{3}$cos2x=1+$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x+$\frac{\sqrt{3}}{2}$=sin(2x+$\frac{π}{3}$)+1+$\frac{\sqrt{3}}{2}$.
∴f(x)的最小正周期T=$\frac{2π}{2}$=π.
(2)∵acosB+bcosA=2ccosC,∴sinAcosB+sinBcosA=2sinCcosC,即sin(A+B)=2sinCcosC.
∴cosC=$\frac{1}{2}$.∴C=$\frac{π}{3}$.
f($\frac{B}{2}$)=sin(B+$\frac{π}{3}$)+1+$\frac{\sqrt{3}}{2}$.∵0<B<$\frac{2π}{3}$,∴当B+$\frac{π}{3}$=$\frac{π}{2}$,即B=$\frac{π}{6}$时,f($\frac{B}{2}$)取得最大值,
∴A=$\frac{π}{2}$.∴b=c•tanB=1,∴S△ABC=$\frac{1}{2}bc$=$\frac{\sqrt{3}}{2}$.
点评 本题考查了三角函数的恒等变换与求值,正弦定理在解三角形中的应用,属于中档题.

 一课一练课时达标系列答案
一课一练课时达标系列答案| A. | ${({\frac{4}{3}})^{n-1}}$ | B. | ${({\frac{3}{4}})^{n-1}}$ | C. | 3n-1 | D. | ${({\frac{1}{3}})^{n-1}}$ |
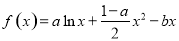 ,
,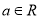 且
且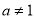 .曲线
.曲线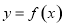 在点
在点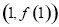 处的切线的斜率为
处的切线的斜率为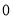 .
.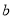 的值;
的值;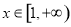 ,使得
,使得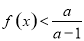 ,求
,求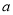 的取值范围.
的取值范围. ,
, ,
, ,若
,若 为实数,
为实数, ,则
,则 ( )
( ) B.
B. C.1 D.2
C.1 D.2