题目内容
过点（4，
）与椭圆
+
=1相切的直线的条数为 ．
| 12 |
| 5 |
| x2 |
| 25 |
| y2 |
| 16 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：把点（4，
）代入椭圆
+
，与1比较可得位置关系．即可得出切线的条数．
| 12 |
| 5 |
| x2 |
| 25 |
| y2 |
| 16 |
解答：
解：∵
+
=1，
∴点（4，
）在椭圆
+
=1上．
点（4，
）与椭圆
+
=1相切的直线的条数为1．
故答案为：1．
| 42 |
| 25 |
| 122 |
| 25×16 |
∴点（4，
| 12 |
| 5 |
| x2 |
| 25 |
| y2 |
| 16 |
点（4，
| 12 |
| 5 |
| x2 |
| 25 |
| y2 |
| 16 |
故答案为：1．
点评：本题考查了点与椭圆的位置关系、椭圆的切线，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
设A、B、C、D是球面上的四点，AB、AC、AD两两互相垂直，且AB=5，AC=4，AD=
，则球的表面积为（ ）
| 23 |
| A、36π | B、64π |
| C、100π | D、144π |
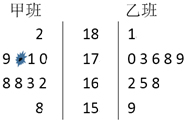随机抽取某中学高三年级甲乙两班各10名同学，测量出他们的身高（单位：cm），获得身高数据的茎叶图如图．其中甲班有一个数据被污损．若圆C的半径为1，点C与点（2，0）关于点（1，0）对称，则圆C的标准方程为（ ）
| A、x2+y2=1 |
| B、（x-3）2+y2=1 |
| C、（x-1）2+y2=1 |
| D、x2+（y-3）2=1 |