题目内容
19.在数列{an}中,a1=2,a2=8,对所有正整数n均有an+2+an=an+1,则$\sum_{n=1}^{2017}$an=2.分析 由递推公式分别求出数列的前8项,由此能求出$\sum_{n-1}^{2017}$an.
解答 解:∵在数列{an}中,a1=2,a2=8,对所有正整数n均有an+2+an=an+1,
∴a3=a2-a1=8-2=6,
a4=a3-a2=6-8=-2,
a5=a4-a3=-2-6=-8,
a6=a8-a4=-8+2=-6,
a7=a6-a5=-6+8=2,
a8=a7-a6=2+6=8,
∴数列{an}是以6为周期的周期数列,
∴$\sum_{n=1}^{2017}$an=336×(2+8+6-2-8-6)+a1=a1=2.
故答案为:2.
点评 本题考查数列的前2017项和的求法,是中档题,解题时要认真审题,注意数列的周期性的合理运用.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
9.设Sn=2+24+27+210+…+23n+10(n∈N+),则Sn=( )
| A. | $\frac{2}{7}$(8n-1) | B. | $\frac{2}{7}$(8n+1-1) | C. | $\frac{2}{7}$(8n+3-1) | D. | $\frac{2}{7}$(8n+4-1) |
7.已知函数$f(x)=\left\{\begin{array}{l}\frac{2}{x},x≥2\\{(x-1)^3},x<2\end{array}\right.$,若关于x的方程f(x)+k=0有两个不同的实根,则实数k的取值范围是( )
| A. | (0,1) | B. | [0,1] | C. | (-1,0) | D. | [-1,0] |
11.抛物线x2=8y的焦点坐标是( )
| A. | (0,$\frac{1}{32}$) | B. | ($\frac{1}{32}$,0) | C. | (2,0) | D. | (0,2) |
8.在△ABC中,角A,B,C的对边分别为a,b,c,∠A,∠B,∠C的大小成等差数列,且a=1,$b=\sqrt{3}$.则∠A的大小为( )
| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $\frac{π}{3}$或$\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
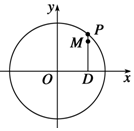 如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为线段PD上一点,且$|{DP}|=\sqrt{2}|{DM}|$.
如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为线段PD上一点,且$|{DP}|=\sqrt{2}|{DM}|$.