题目内容
4.函数f(x)=2sinx的定义域和值域都是[a,b],这样的区间[a,b]有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 不存在 |
分析 结合函数y=2sinx的值域是[-2,2],可得[a,b]⊆[-2,2],考虑函数y=2sinx在区间[a,b]上单调性,结合a<b即可得.
解答 解:在同一坐标系中作出函数y=2sinx和函数y=x的图象如下图所示:
由图可知:f(x)=2sinx的定义域和值域都是[a,b],这样的区间[a,b]有
[-2,0],[0,2],[-2,2]共3个,
故选:C.
点评 本题考查的知识点是正弦函数的图象和性质,正确理解定义域和值域都是[a,b],是解答的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
9.三对夫妻站成一排照相,则仅有一对夫妻相邻的站法总数是( )
| A. | 72 | B. | 144 | C. | 240 | D. | 288 |
16.已知集合A={x|x=sin$\frac{nπ}{6}$,n∈z},则该集合中所有元素之和为( )
| A. | -3-$\sqrt{3}$ | B. | 0 | C. | $\frac{3+\sqrt{3}}{2}$ | D. | 3+$\sqrt{3}$ |
4.阅读如图所示的程序框图,运行相应的程序,输出的n的值等于( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
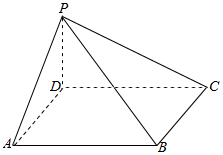 如图所示,四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠DAB=60°,PA=PB=PD=a.
如图所示,四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠DAB=60°,PA=PB=PD=a.