题目内容
13.F1,F2分别为椭圆$\frac{x^2}{36}+\frac{y^2}{27}$=1的左、右焦点,A为椭圆上一点,且$\overrightarrow{OB}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{{OF}_{1}}$),$\overrightarrow{OC}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{{OF}_{2}}$),则|$\overrightarrow{OB}$|+|$\overrightarrow{OC}$|6.分析 求得椭圆的a=6,运用椭圆的定义可得|AF1|+|AF2|=2a=12,由向量的中点表示形式,可得B为AF1的中点,C为AF2的中点,运用中位线定理和椭圆定义,即可得到所求值.
解答 解:椭圆$\frac{x^2}{36}+\frac{y^2}{27}$=1的a=6,
由椭圆的定义可得|AF1|+|AF2|=2a=12,
$\overrightarrow{OB}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{{OF}_{1}}$),可得B为AF1的中点,
$\overrightarrow{OC}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{O{F}_{2}}$),可得C为AF2的中点,
由中位线定理可得|OB|=$\frac{1}{2}$|AF2|,
|OC|=$\frac{1}{2}$|AF1|,
即有|$\overrightarrow{OB}$|+|$\overrightarrow{OC}$|=$\frac{1}{2}$(|AF1|+|AF2|)=a=6,
故答案为:6.
点评 本题考查椭圆的定义、方程和性质,考查向量的中点表示形式,同时考查中位线定理,运用椭圆的第一定义是解题的关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.函数f(x)=2sinx的定义域和值域都是[a,b],这样的区间[a,b]有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 不存在 |
8.已知复数z=$\frac{1}{1+i}$+i3(i为虚数单位),则z的虚部为( )
| A. | $\frac{3}{2}$ | B. | $\frac{3}{2}$i | C. | -$\frac{3}{2}$i | D. | -$\frac{3}{2}$ |
12.已知i为虚数单位,复数z满足(1-3i)z=10(1+i),则|z|=( )
| A. | $\sqrt{5}$ | B. | 5 | C. | 2$\sqrt{5}$ | D. | 20 |
13.汽车业是碳排放量比较大的行业之一,欧盟规定,从2012年开始,将对二氧化碳排放量超过130g/km的M1型汽车进行惩罚,某检测单位对甲、乙两类M1型品牌汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:g/km)
经测算发现,乙品牌M1型汽车二氧化碳排放量的平均值为 $\overline{x_乙}=120g/km$
(Ⅰ)从被检测的5辆甲类M1型品牌车中任取2辆,则至少有1辆二氧化碳排放量超过130g/km的概率是多少?
(Ⅱ)求表中x的值,并比较甲、乙两品牌M1型汽车二氧化碳排放量的稳定性.
(${s^2}=\frac{1}{n}[{(\overline x-{x_1})^2}+{(\overline x-{x_2})^2}+…+{(\overline x-{x_n})^2}]$其中,$\overline x$表示的平均数,n表示样本的数量,xi表示个体,s2表示方差)
| 甲 | 80 | 110 | 120 | 140 | 150 |
| 乙 | 100 | 120 | x | 100 | 160 |
(Ⅰ)从被检测的5辆甲类M1型品牌车中任取2辆,则至少有1辆二氧化碳排放量超过130g/km的概率是多少?
(Ⅱ)求表中x的值,并比较甲、乙两品牌M1型汽车二氧化碳排放量的稳定性.
(${s^2}=\frac{1}{n}[{(\overline x-{x_1})^2}+{(\overline x-{x_2})^2}+…+{(\overline x-{x_n})^2}]$其中,$\overline x$表示的平均数,n表示样本的数量,xi表示个体,s2表示方差)
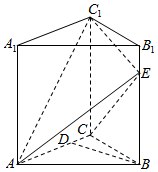 如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=2$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上一点,BD∥平面AC1E.
如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=2$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上一点,BD∥平面AC1E.