题目内容
10.数列{an}满足a1=$\frac{1}{3}$,且对任意n∈N*,an+1=an2+an,cn=$\frac{1}{{{a_n}+1}}$,数列{cn}的前n项和为Sn,则S2017的整数部分是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 an+1=${a}_{n}^{2}$+an,a1=$\frac{1}{3}$.可得an+1>an,a4>1.即n≥4时,$\frac{1}{{a}_{n}}$∈(0,1).由an+1=${a}_{n}^{2}$+an,可得:$\frac{1}{{a}_{n}+1}$=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$,即cn=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$,利用“裂项求和”方法即可得出.
解答 解:∵an+1=${a}_{n}^{2}$+an,a1=$\frac{1}{3}$,∴an+1>an.
∴a2=$\frac{1}{9}$+$\frac{1}{3}$=$\frac{4}{9}$,a3=$(\frac{4}{9})^{2}$+$\frac{4}{9}$=$\frac{52}{81}$,a4=$(\frac{52}{81})^{2}$+$\frac{52}{81}$=$\frac{6916}{6561}$>1.
∴n≥4时,$\frac{1}{{a}_{n}}$∈(0,1).
∵an+1=${a}_{n}^{2}$+an,∴$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n}+1}$,可得:$\frac{1}{{a}_{n}+1}$=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$,
∴cn=$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$,
∴数列{cn}的前n项和Sn=$(\frac{1}{{a}_{1}}-\frac{1}{{a}_{2}})$+$(\frac{1}{{a}_{2}}-\frac{1}{{a}_{3}})$+…+$(\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}})$=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{n+1}}$.
∴S2017=$\frac{1}{{a}_{1}}$-$\frac{1}{{a}_{2018}}$=3-$\frac{1}{{a}_{2018}}$∈(2,3).
其整数部分为2.
故选:B.
点评 本题考查了数列递推关系、裂项求和方法、数列的单调性、实数的性质,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | -3≤m≤3 | B. | -6≤m≤6 | C. | -3≤m≤6 | D. | -6≤m≤0 |
| A. | (0,+∞) | B. | (1,+∞) | C. | [0,+∞) | D. | [1,+∞) |
| A. | 81 | B. | 90 | C. | 100 | D. | 121 |
| A. | -2 | B. | -4 | C. | 2 | D. | 4 |
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD,E,F分别为PD,BC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD,E,F分别为PD,BC的中点.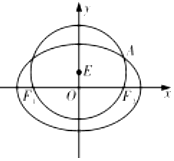 如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,已知圆E:x2+(y-1)2=4经过椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.