题目内容
已知动圆M和圆C1：（x+1）2+y2=36内切，并和圆C2：（x-1）2+y2=4外切，动圆圆心M的轨迹方程为 ．
考点：轨迹方程
专题：圆锥曲线的定义、性质与方程
分析：设动圆的半径为r，由已知得到动圆圆心满足到两定圆的圆心的距离和为定值，且大于两定圆的圆心距，由题意定义得答案．
解答：
解：如图，
设动圆的半径为r，根据题意，|MC1|=6-r，|MC2|=2+r，
∴|MC1|+|MC2|=8，即2a=8，a=4．
又|C1C2|=2，2c=2，c=1，
∴b2=16-1=15．
∴圆心M的轨迹为椭圆，其方程为
+
=1．
故答案为：
+
=1．
设动圆的半径为r，根据题意，|MC1|=6-r，|MC2|=2+r，
∴|MC1|+|MC2|=8，即2a=8，a=4．
又|C1C2|=2，2c=2，c=1，
∴b2=16-1=15．
∴圆心M的轨迹为椭圆，其方程为
| x2 |
| 16 |
| y2 |
| 15 |
故答案为：
| x2 |
| 16 |
| y2 |
| 15 |
点评：本题考查了两圆间的位置关系的应用，考查了椭圆的定义及标准方程，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
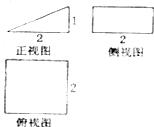
锐角△ABC的内心为I，过点A作直线BI的垂线，垂足为H，点E为内切圆I与边CA的切点．若∠C=50°，则∠IEH的度数=一个几何体的三视图如图所示，则这个几何体的表面积为（ ）
A、6+
| ||
B、6+2
| ||
C、8+
| ||
D、8+2
|
已知x、y的取值如表：从散点图分析，y与x线性相关，且回归方程为
=0.95x+a，则a=（ ）
 |
| y |
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A、2.6 | B、4 |
| C、4.5 | D、条件不足，无法求解 |