题目内容
指出下列各椭圆的中心、焦点坐标、顶点坐标、长半轴长、短半轴长和离心率.
(1)
+
=1;
(2)
+
=1;
(3)4x2+9y2=1.
(1)
| x2 |
| 6 |
| y2 |
| 9 |
(2)
| x2 |
| 169 |
| y2 |
| 144 |
(3)4x2+9y2=1.
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:椭圆方程化为标准方程,确定几何量,即可得到椭圆的性质.
解答:
解:(1)椭圆的标准方程为
+
=1,
∴a2=9,b2=6,c2=3,
∴a=3,b=
,c=
,
∴椭圆的中心是(0,0),焦点坐标(0,±
)、顶点坐标(0,±3),(±
,0)、长半轴3,短半轴
,离心率e=
=
.
(2)∵
+
=1,
∴a2=169,b2=144,c2=25,
∴a=13,b=12,c=5,
∴椭圆的中心是(0,0),焦点坐标(±5,0)、顶点坐标(0,±12),(±13,0)、长半轴13,短半轴12,离心率e=
=
.
(3)椭圆的标准方程为
+
=1,
∴a2=
,b2=
,c2=
,
∴a=
,b=
,c=
,
∴椭圆的中心是(0,0),焦点坐标(±
,0)、顶点坐标(0,±
),(±
,0)、长半轴
,短半轴
,离心率e=
=
.
| x2 |
| 6 |
| y2 |
| 9 |
∴a2=9,b2=6,c2=3,
∴a=3,b=
| 6 |
| 3 |
∴椭圆的中心是(0,0),焦点坐标(0,±
| 3 |
| 6 |
| 6 |
| c |
| a |
| ||
| 3 |
(2)∵
| x2 |
| 169 |
| y2 |
| 144 |
∴a2=169,b2=144,c2=25,
∴a=13,b=12,c=5,
∴椭圆的中心是(0,0),焦点坐标(±5,0)、顶点坐标(0,±12),(±13,0)、长半轴13,短半轴12,离心率e=
| c |
| a |
| 5 |
| 13 |
(3)椭圆的标准方程为
| x2 | ||
|
| y2 | ||
|
∴a2=
| 1 |
| 4 |
| 1 |
| 9 |
| 5 |
| 36 |
∴a=
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 6 |
∴椭圆的中心是(0,0),焦点坐标(±
| ||
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| c |
| a |
| ||
| 3 |
点评:本题考查椭圆的方程,考查椭圆的几何性质,确定几何量是关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
函数y=(m2+2m-2)x
是幂函数,则m=( )
| 1 |
| m-1 |
| A、1 | B、-3 | C、-3或1 | D、2 |
 已知在平行六面体ABCD-A1B1C1D1中.
已知在平行六面体ABCD-A1B1C1D1中.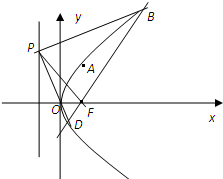 在平面直角坐标系xOy中,抛物线C的顶点在原点,经过点A(1,2)其焦点F在x轴上.
在平面直角坐标系xOy中,抛物线C的顶点在原点,经过点A(1,2)其焦点F在x轴上.