题目内容
已知数列{an}中,a1=
,an≠0,且an=
(n≥2),则a2009=( )
| 3 |
| 2 |
| 3an-1 |
| 3+2an-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列递推式
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:根据数列的递推关系,利用取倒数法求出数列的通项公式即可得到结论.
解答:
解:∵an=
(n≥2),
∴两边取倒数得
=
=
+
,
则
-
=
,
即数列{
}是公差d=
的等差数列,首项为
=
,
则
=
+
(n-1)=
n,
则an=
,
则a2009=
=
,
故选:C
| 3an-1 |
| 3+2an-1 |
∴两边取倒数得
| 1 |
| an |
| 3+2an-1 |
| 3an-1 |
| 1 |
| an-1 |
| 2 |
| 3 |
则
| 1 |
| an |
| 1 |
| an-1 |
| 2 |
| 3 |
即数列{
| 1 |
| an |
| 2 |
| 3 |
| 1 |
| a1 |
| 2 |
| 3 |
则
| 1 |
| an |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
则an=
| 3 |
| 2n |
则a2009=
| 3 |
| 2×2009 |
| 3 |
| 4018 |
故选:C
点评:本题主要考查数列通项公式的求解,利用求倒数法以及等差数列的性质是解决本题的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
已知命题p:“若直线ax+y+1=0与直线ax-y+2=0垂直,则a=1”;命题q:“a
<b
”是“a<b”的充要条件,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、p真,q假 |
| B、“p∧q”真 |
| C、“p∨q”真 |
| D、“p∨q”假 |
已知两个单位向量
,
的夹角为60°,
=(1-t)
+t
,若
•
=-
,则实数t的取值是( )
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
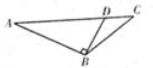
如图,在△ABC中,点D在AC上,AB⊥BD,BC=3
,BD=5,sin∠ABC=
,则CD的长为( )
| 3 |
2
| ||
| 5 |

A、
| ||
| B、4 | ||
C、2
| ||
| D、5 |
设二项式(x-
)4的展开式中常数项为A,则A=( )
| 1 | |||
|
| A、-6 | B、-4 | C、4 | D、6 |
 如图所示的是正方形的顶点A为圆心,边长为半径的画弧形成的图象,现向正方形内投掷一颗豆子(假设豆子不落在线上),则恰好落在阴影部分的概率为
如图所示的是正方形的顶点A为圆心,边长为半径的画弧形成的图象,现向正方形内投掷一颗豆子(假设豆子不落在线上),则恰好落在阴影部分的概率为