题目内容

计算：
∫
5
1
（|2-x|+|sinx|）dx．
考点：定积分
专题：导数的综合应用
分析：利用x的范围，将被积函数的绝对值去掉．
解答： 解：
∫
5
1
（|2-x|+|sinx|）dx=
∫
2
1
(2-x)dx+
∫
5
2
(x-2)dx+
∫
π
1
sinxdx+
∫
5
π
(-sinx)dx
=（2x-
1
2
x2）|
 
2
1
+（
1
2
x2-2x|
 
5
2
+（-cosx）|
 
π
1
+cosx|
 
5
π

=4-2-2+
1
2
+
25
2
-10-2+4+1+cos1+cos5+1
=7+cos1+cos5．
点评：本题考查了定积分的计算以及定积分的运算法则的运用．
练习册系列答案
相关题目
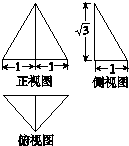一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的表面积为
 
．
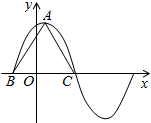已知函数f（x）=
2-2x，x≤-1
2x+2，x＞-1
，则满足f（a）≥2的实数a的取值范围是
 
．
执行如图所示的程序框图，则输出的结果是
 
；
已知等差数列{an}的前n项和为Sn，S7=49，5是a1和a5的等差中项．
（1）求an与Sn
（2）证明：当n≥2时，有
1
S1
+
1
S2
+…+
1
Sn
＜
7
4
．
已知函数f（x）=
3
acos2
ωx
2
+
1
2
asinωx-
3
2
a（ω＞0，a＞0在一个周期内的图象如图所示，其中点A为图象上的最高点，点B，C为图象与x轴的两个相邻交点，且△ABC是边长为4的正三角形．
（1）求ω与a的值；
（2）若f（x0）=
8
3
5
，且x0∈（-
10
3
，
2
3
），求f（x0+1）的值．
已知△ABC的面积为2，且满足0＜
AB
•
AC
≤4，设
AB
和
AC
的夹角为θ．
（1）求θ的取值范围；
（2）求函数f（θ）=2sin2（
π
4
+θ）-
3
cos2θ的取值范围．
已知cos（
π
6
+α）=
3
3
，求sin（
π
3
-α）的值．
在△ABC中，角A，B，C所对的边分别是a，b，c，已知
a
3
cosA
=
c
sinC
=
a
sinA
．
（1）求A的大小；
（2）若a=6，求b+c的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网