题目内容
已知A={x|x2-x-2=0}，B={x|x2+4x+p=0}，若B⊆A，则实数p的取值范围是 ．
考点：集合的包含关系判断及应用
专题：集合
分析：先求出A，因为B⊆A，所以B分成B=∅，和B≠∅两种情况．B=∅时，能求p的范围；B≠∅时，又分方程x2+4x+p=0有一个根和两个根的情况，从而求出对应的p的取值，这样就能求出p的取值范围了．
解答：
解：A={-1，2}
∵B⊆A
∴B=∅时满足B⊆A，此时16-4p＜0，解得p＞4；
B≠∅时，方程x2+4x+p=0有一个根，或两个根
∵对于方程x2+4x+p=0，x1+x2=-4，∴-1，2不是该方程的根，∴这种情况不存在．
∴p的取值范围是（4，+∞）．
故答案是：（4，+∞）．
∵B⊆A
∴B=∅时满足B⊆A，此时16-4p＜0，解得p＞4；
B≠∅时，方程x2+4x+p=0有一个根，或两个根
∵对于方程x2+4x+p=0，x1+x2=-4，∴-1，2不是该方程的根，∴这种情况不存在．
∴p的取值范围是（4，+∞）．
故答案是：（4，+∞）．
点评：本题考查子集的概念，方程的根与方程系数的关系，不要漏了B=∅的情况．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
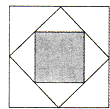任意画一个正方形，再将这个正方形各边的中点相连得到第二个正方形，依此类推，这样一共画了3个正方形，如图所示．若向图形中随机投一点，则所投点落在第三个正方形的概率是