题目内容

9．已知数列{an}的通项公式为an=$\frac{n-\sqrt{51}}{n-\sqrt{52}}$，则在数列{an}的前30项中，最大项和最小项分别是（　　）
A．a30，a1B．a1，a30C．a8，a30D．a8，a7

分析 把给出的数列的通项公式变形，把an看作n的函数，作出相应的图象，由图象分析得到答案．

解答 解：an=$\frac{n-\sqrt{51}}{n-\sqrt{52}}$，
∴an=$\frac{n-\sqrt{52}-\sqrt{51}+\sqrt{52}}{n-\sqrt{52}}$=1+$\frac{\sqrt{52}-\sqrt{51}}{n-\sqrt{52}}$，
当1≤n≤7时，an单调递减，且a7＜1为最小；
当8≤n≤30时，an单调递减，且a8＞1为最大．
∴这个数列的前30项中最大项和最小项分别是a8，a7．
故答案选：D．

点评 本题考查了利用函数的单调性求数列的最大值与最小值，属于中档题．

练习册系列答案
相关题目
19．设函数f（x）=a1sin（x+a1）+a2sin（x+a2）+…+ansin（x+an），其中ai，aj（i=1，2，…，n，n∈N*，n≥2）为已知实常数，x∈R，下列关于函数f（x）的性质判断正确的个数是（　　）
①若f（0）=f（$\frac{π}{2}$）=0，则f（x）=0对任意实数x恒成立；
②若f（0）=0，则函数f（x）为奇函数；
③若f（$\frac{π}{2}$）=0，则函数f（x）为偶函数；
④当f2（0）+f2（$\frac{π}{2}$）≠0时，若f（x1）=f（x2）=0，则x1-x2=kπ（k∈Z）
A．4B．3C．2D．1
20．设两条直线的方程分别为x+y+a=0，x+y+b=0，已知a，b是方程x2+x+c=0的两个实根，且0≤c≤$\frac{1}{8}$，则这两条直线之间的距离的取值范围是[$\frac{1}{2}$，$\frac{\sqrt{2}}{2}$]．
17．如图，在三棱柱ABM-DCN中，侧面ADNM⊥侧面ABCD，且侧面ADNM是矩形，AD=2，AM=1，侧面ABCD是菱形，∠DAB=60°，E是AB的中点．
（1）求证：AN∥平面MEC；
（2）求三棱锥E-CMN的体积．
4．若一圆锥的侧面积为15π，体积是12π，则该圆锥的底面半径等于3．
14．执行如图所示的程序框图，输出的n为（　　）
A．3B．4C．5D．6
1．如图是某算法的程序框图，若输出y值为4，则输入的x最大负整数是（　　）
A．-3B．-2C．-1D．-4
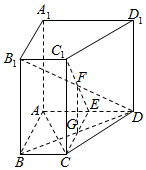18．如图，在四棱柱ABCD-A1B1C1D1中，AC⊥B1D，BB1⊥底面ABCD，E为线段AD上的任意一点（不包括A、D两点），平面CEC1与平面BB1D交于FG．
（1）证明：AC⊥BD；
（2）证明：FG∥平面AA1B1B．
19．某人上午7时乘摩托艇以匀速v n mile/h（4 n mile/h≤t≤20 n mile/h）从A港出发到距50 n mile的B港，然后乘汽车以匀速ω km/h（30 km/h≤ω≤100 km/h）自B港向距300km的C市驶去，应该在同一天下午4点至9点到达C市．设汽车、摩托艇所需的时间分别是x h和y h，所需要的经费P=100+3•（5-x）+2•（8-y）元，求v、ω分别是多少时走的最经济？此时需要花费多少元？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网