题目内容
函数f(x)=
,若方程f(x)=mx恰有四个不同的实数根,则实数m的取值范围为( )
|
A、(8-2
| ||||
B、(4+2
| ||||
C、(4-2
| ||||
D、(8-2
|
考点:分段函数的应用
专题:计算题,数形结合,函数的性质及应用
分析:通过x>1是周期函数,画出函数y=f(x)的图象和函数y=mx的图象,通过图象观察,考虑直线绕着原点旋转,分析直线与1<x<3的图象相切和3<x<5的图象相切情况,求出此时的m的值,从而判断满足条件的实数m的取值范围.
解答:
解:当1<x≤3时,-1<x-2≤1,f(x-2)=1-(x-2)2,即f(x)=1-(x-2)2,
当3<x≤5时,-1<x-4≤1,f(x-4)=1-(x-4)2,即f(x)=1-(x-4)2,
…
画出函数y=f(x)的图象和函数y=mx的图象,
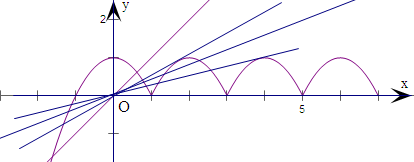
由
消去y得,x2-(4-m)x+3=0,由判别式等于0,(4-m)2-12=0,m=4±2
,
检验m=4+2
时,x=-
不成立,故m=4-2
;
由
消去y得,x2-(8-m)x+15=0,由判别式为0,(8-m)2-60=0,m=8±2
,
检验m=8+2
时,x=-
不成立,故m=8-2
.
故方程f(x)=mx恰有四个不同的实数根,则实数m的取值范围为(8-2
,4-2
).
故选A.
当3<x≤5时,-1<x-4≤1,f(x-4)=1-(x-4)2,即f(x)=1-(x-4)2,
…
画出函数y=f(x)的图象和函数y=mx的图象,

由
|
| 3 |
检验m=4+2
| 3 |
| 3 |
| 3 |
由
|
| 15 |
检验m=8+2
| 15 |
| 15 |
| 15 |
故方程f(x)=mx恰有四个不同的实数根,则实数m的取值范围为(8-2
| 15 |
| 3 |
故选A.
点评:本题考查函数的周期性及运用,考查方程的根的个数转化为函数的图象交点个数,注意通过图象观察,主要是直线旋转与曲线的交点问题,属于中档题.

练习册系列答案
相关题目
7人站成一排,其中甲不排头,乙不排当中的不同排法种数为( )
| A、4000 | B、3720 |
| C、960 | D、1024 |
命题“对任意x∈R,都有2x>0”的否定是( )
| A、对任意x∈R,都有2x≤0 |
| B、不存在x∈R,使得2x≤0 |
| C、存在x0∈R,使得2x>0 |
| D、存在x0∈R,2x0≤0 |
有下列调查方式:
①学校为了解高一学生的数学学习情况,从每班抽2人进行座谈;
②一次数学竞赛中,某班有15人在100分以上,35人在90~100分,10人低于90分.现在从中抽取12人座谈了解情况;
③运动会中工作人员为参加400m比赛的6名同学公平安排跑道.
就这三个调查方式,最合适的抽样方法依次为( )
①学校为了解高一学生的数学学习情况,从每班抽2人进行座谈;
②一次数学竞赛中,某班有15人在100分以上,35人在90~100分,10人低于90分.现在从中抽取12人座谈了解情况;
③运动会中工作人员为参加400m比赛的6名同学公平安排跑道.
就这三个调查方式,最合适的抽样方法依次为( )
| A、分层抽样,系统抽样,简单随机抽样 |
| B、系统抽样,系统抽样,简单随机抽样 |
| C、分层抽样,简单随机抽样,简单随机抽样 |
| D、系统抽样,分层抽样,简单随机抽样 |
已知an=n(n+1),以下四个数中,哪个是数列{an}中的一项( )
| A、18 | B、21 | C、25 | D、30 |
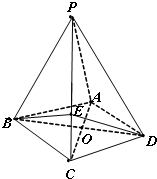 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD.PA=AB=2,∠BAD=120°,E是PC上的一点,且BE与平面PAB所成角的正弦值为
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD.PA=AB=2,∠BAD=120°,E是PC上的一点,且BE与平面PAB所成角的正弦值为