题目内容

（文）若sin2α=
1
3
，则cos2（α+
π
4
）=（　　）
A、
2
3
B、
1
2
C、
1
3
D、
1
6
考点：二倍角的余弦
专题：三角函数的求值
分析：根据 sin2α=
1
3
，利用二倍角公式求得cos2（α+
π
4
）=
1-sin2α
2
，计算求得结果．
解答： 解：∵sin2α=
1
3
，则cos2（α+
π
4
）=
1+cos(2α+
π
2
)
2
=
1-sin2α
2
=
1
3
，
故选：C．
点评：本题主要考查二倍角的余弦公式的应用，属于中档题．
练习册系列答案
相关题目
已知复数z=
2
+t
(1-
2
t)2
，则|z|=（　　）
A、2
B、
2
3
3
C、
3
3
D、
3
已知函数f（x）=sin（2x+φ），其中f（x）≤|f（
π
6
）|对x∈R恒成立，且f（
π
2
）＜f（π），则f（x）的单调递增区间是（　　）
A、[kπ+
π
6
，kπ+
2π
3
]（k∈Z）
B、[kπ，kπ+
π
2
]（k∈Z）
C、[kπ-
π
3
，kπ+
π
6
]（k∈Z）
D、[kπ-
π
2
，kπ]（k∈Z）
已知x，y，z均为复数，则x+z＞2y是x+z-2y＞0成立的什么条件（　　）
A、充分不必要条件
B、必要不充分条件
C、充分必要条件
D、既不充分也不必要条件
已知变量x，y满足约束条件
x+2y≥0
x-y≥0
0≤x≤3
，则z=x+y的最大值为（　　）
A、3B、4C、5D、6
“a=1”是“关于x的方程x2-2x+a=0有实数根”的（　　）
A、充分而不必要条件
B、必要而不充分条件
C、充要条件
D、既不充分也不必要条件
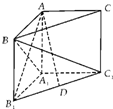如图，在直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=AC=AA1．
（1）求证：AB1⊥平面A1BC1；
（2）若D为B1C1的中点，求异面直线AD与A1B所成的角的大小．
已知A箱装有编号为1，2，3，4，5的五个小球（小球除编号不同之外，其他完全相同），B箱装有编号为2，4的两个小球（小球除编号不同之外，其他完全相同），甲从A箱中任取一个小球，乙从B箱中任取一个小球，用X，Y分别表示甲，乙两人取得的小球上的数字．
（1）求概率P（X＞Y）；
（2）设随机变量ξ=
X，X≥Y
Y，X＜Y
，求ξ的分布列及数学期望．
从0，1，2，…，9这10个整数中任意取3个不同的数作为二次函数f（x）=ax2+bx+c的系数，则使得
f(1)
2
∈Z的概率为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网