题目内容
下列四个函数中，在（0，+∞）上是减函数的是（ ）
| A、f（x）=x+3 | ||
| B、f（x）=（x-1）2 | ||
C、f（x）=
| ||
| D、f（x）=|x| |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：根据一次函数，二次函数，反比例函数，绝对值函数的单调性，分别判断四个函数的在（0，+∞）上的单调性，可得答案
解答：
解：A中，f（x）=x+3在（0，+∞）上是增函数，不满足要求；
B中，f（x）=（x-1）2在（0，+∞）上是增函数，不满足要求；
C中，f（x）=
+1在（0，+∞）上是减函数，满足要求；
在中，f（x）=|x|在（0，+∞）上是增函数，不满足要求；
故选：C
B中，f（x）=（x-1）2在（0，+∞）上是增函数，不满足要求；
C中，f（x）=
| 1 |
| x |
在中，f（x）=|x|在（0，+∞）上是增函数，不满足要求；
故选：C
点评：本题考查复合函数的单调性、指数函数、对数函数及一次函数的性质，属中档题．
练习册系列答案
相关题目
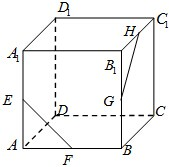如图，在正方体ABCDA1B1C1D1中，E、F、G、H分别为AA1、AB、BB1、BC1的中点，则异面直线EF与GH所成的角等于（ ）| A、30° | B、45° |
| C、60° | D、90° |
根据如图所示各图中三角形的个数，推断第10个图中三角形的个数是（ ）
| A、60 | B、62 | C、65 | D、66 |
在△ABC中，已知sinB=2sin（B+C）cosC，那么△ABC一定是（ ）
| A、等腰直角三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等边三角形 |
点S，A，B，C是球O的球面上的四个点，S，O在平面ABC的同侧，∠ABC=120°，AB=BC=2，平面SAC⊥平面ABC，若三棱锥S-ABC的体积为
，则该球的表面积为（ ）
| 3 |
| A、18π | B、16π |
| C、20π | D、25π |
根据如图所示的程序框图，若输出的结果T=600，则图中横线上应填（ ）
| A、48 | B、50 | C、52 | D、54 |