题目内容
14.已知a∈($\frac{2}{3}$,1),函数f(x)=x3-$\frac{3}{2}$ax2+b,x∈[-1,1],f(x)${\;}_{{\;}_{min}}$=1,f(x)max=$\frac{\sqrt{6}}{2}$,求a,b的值.分析 求出导数,求得极值点,求出极值和端点的函数值,比较可得f(0)最大,f(-1)最小,解方程可得a,b的值.
解答 解:函数f(x)=x3-$\frac{3}{2}$ax2+b的导数为f′(x)=3x2-3ax=3x(x-a),
由f′(x)=0,可得x=0或a,
由f(0)=b,f(a)=b-$\frac{1}{2}$a3,f(-1)=-1-$\frac{3}{2}$a+b,f(1)=1-$\frac{3}{2}$a+b,
由a∈($\frac{2}{3}$,1),可得f(0)>f(1),f(-1)<f(1),f(0)>f(a),
则f(0)为最大值,且为b=$\frac{\sqrt{6}}{2}$;
由$\frac{2}{3}$<a<1,可得f(-1)-f(a)=$\frac{1}{2}$a3-1-$\frac{3}{2}$a<0,
则f(-1)<f(a),即有f(-1)为最小值,即为-1-$\frac{3}{2}$a+$\frac{\sqrt{6}}{2}$=-1,
解得a=$\frac{\sqrt{6}}{3}$.
综上可得,a=$\frac{\sqrt{6}}{3}$,b=$\frac{\sqrt{6}}{2}$.
点评 本题考查函数的最值的求法,注意运用导数,求出极值和端点的函数值,考查运算能力,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
4.已知集合B={x|-3<x<2},C={x|2x-1≥0}.
(1)求B∩C,B∪C;
(2)设函数f(x)=$\sqrt{lo{g}_{2}(2x+m)}$的定义域为A,且A⊆C,求实数m的最大值.
(1)求B∩C,B∪C;
(2)设函数f(x)=$\sqrt{lo{g}_{2}(2x+m)}$的定义域为A,且A⊆C,求实数m的最大值.
2.直线l与平面α垂直的一个充分条件是( )
| A. | l垂直于平面α内的一条直线 | B. | l垂直于平面α内的两条直线 | ||
| C. | l垂直于平面α内的无数条直线 | D. | l垂直于平面α内的任一条直线 |
19.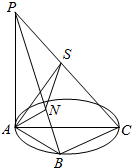 如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )
如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )
 如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )
如图,AC为圆O的直径,B为圆周上不与点A、C重合的点,PA垂直于圆O所在的平面,连结PB、PC、AB、BC,作AN⊥PB,AS⊥PC,连结SN,则图中直角三角形个数为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
6.若$\frac{5π}{2}$<α<3π,则$\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}cosα}}$等于( )
| A. | cos$\frac{α}{4}$ | B. | -cos$\frac{α}{4}$ | C. | sin$\frac{α}{4}$ | D. | -sin$\frac{α}{4}$ |
3.在区间[0,2]上任取两个实数a、b,则函数f(x)=x2+ax-$\frac{1}{4}$b2+1在区间(-1,1)没有零点的概率为( )
| A. | $\frac{π}{8}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{4-π}{8}$ | D. | $\frac{π}{4}$ |
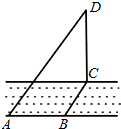 如图,在河的一侧有一塔CD=12m,河宽BC=3m,另一侧有点A,AB=4m,则点A与塔顶D的距离AD=13.
如图,在河的一侧有一塔CD=12m,河宽BC=3m,另一侧有点A,AB=4m,则点A与塔顶D的距离AD=13.