题目内容
设G,M分别为不等边三角形ABC的重心和外心,A(-1,0),B(1,0),且
∥
(1)求点C的轨迹P的方程;
(2)是否存在直线L过点(0,1),并与曲线P交于R,T两点,且满足
•
=0,若存在,求出直线L的方程,若不存在,说明理由.
| GM |
| AB |
(1)求点C的轨迹P的方程;
(2)是否存在直线L过点(0,1),并与曲线P交于R,T两点,且满足
| OR |
| OT |
考点:轨迹方程,平面向量数量积的运算
专题:
分析:(1)可设C点的坐标为(x,y),由重心坐标的公式,可得G(
x,
y),再由外心M在AB的垂直平分线上,而AB所在直线为y=0,外心就落在y轴上,横坐标为零,则可设外心坐标M(0,b),由GM∥AB可得M(0,
y),由外心定义,CM=AM=BM,AM已经等于Bm了,只需要令CM=AM或者CM=BM即可,代入距离公式可求点C的轨迹方程.
(2)假设存在直线l满足条件,设直线l方程为y=kx+1,联立直线与椭圆的方程,由
•
=0,根据方程的根与系数的关系代入可求k,即可求出直线L的方程.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)假设存在直线l满足条件,设直线l方程为y=kx+1,联立直线与椭圆的方程,由
| OR |
| OT |
解答:
解:(1)设C(x,y)(xy≠0),则
由重心坐标的公式,可得G(
x,
y)
外心M在AB的垂直平分线上,显然AB所在直线为y=0,外心就落在y轴上,横坐标为零;
设外心坐标M(0,b),由GM∥AB可知
y=b
那么就确定了外心坐标M(0,
y)
由外心定义,CM=AM=BM,AM已经等于Bm了,只需要令CM=AM或者CM=BM即可
不妨CM=AM,
∴x2+(y-
y)2=(-1-0)2+(
y)2,
整理可得点C的轨迹方程为x2+
=1(xy≠0);
(2)假设存在直线l满足条件,设直线l方程为y=kx+1,
与x2+
=1联立,消去x,得(3+k2)x2+2kx-2=0
∵直线l与曲线P交于R,T两点两点,∴△=4k2+8(2+k2)>0
设PRx1,y1),T(x2,y2),则x1+x2=-
,x1x2=-
,
∵
•
=0,
∴x1x2+y1y2=0,即x1x2+(kx1+1)(kx2+1)=0.
(1+k2)x1x2+k(x1+x2)+1=0,(1+k2)(-
)+k(-
)+1=0
解得k2=
,∴k=±
故存在直线l:y=±
+1,使得
•
=0.
由重心坐标的公式,可得G(
| 1 |
| 3 |
| 1 |
| 3 |
外心M在AB的垂直平分线上,显然AB所在直线为y=0,外心就落在y轴上,横坐标为零;
设外心坐标M(0,b),由GM∥AB可知
| 1 |
| 3 |
那么就确定了外心坐标M(0,
| 1 |
| 3 |
由外心定义,CM=AM=BM,AM已经等于Bm了,只需要令CM=AM或者CM=BM即可
不妨CM=AM,
∴x2+(y-
| 1 |
| 3 |
| 1 |
| 3 |
整理可得点C的轨迹方程为x2+
| y2 |
| 3 |
(2)假设存在直线l满足条件,设直线l方程为y=kx+1,
与x2+
| y2 |
| 3 |
∵直线l与曲线P交于R,T两点两点,∴△=4k2+8(2+k2)>0
设PRx1,y1),T(x2,y2),则x1+x2=-
| 2k |
| 3+k2 |
| 2 |
| 3+k2 |
∵
| OR |
| OT |
∴x1x2+y1y2=0,即x1x2+(kx1+1)(kx2+1)=0.
(1+k2)x1x2+k(x1+x2)+1=0,(1+k2)(-
| 2 |
| 3+k2 |
| 2k |
| 3+k2 |
解得k2=
| 1 |
| 3 |
| ||
| 3 |
故存在直线l:y=±
| ||
| 3 |
| OR |
| OT |
点评:本题主要考查了三角形的外心与重心性质的应用,点的轨迹方程的求解,直线与椭圆相交关系中的方程的根与系数关系的应用及一定的推理与运算的能力的考查,具有一定的综合性.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
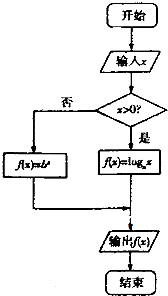 在如图所示的程序框图中,当输入实数x的值为4时,输出的结果为2;当输入实数x的值为-2时,输出的结果为4.
在如图所示的程序框图中,当输入实数x的值为4时,输出的结果为2;当输入实数x的值为-2时,输出的结果为4. 某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了100名学生的成绩,得到如图所示的成绩频率分布直方图.
某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了100名学生的成绩,得到如图所示的成绩频率分布直方图.