题目内容
14. 某建筑工地在一块唱AM=30米,宽AN=20米的矩形地块AMPN上施工,规划建设占地如图中矩形ABCD的学生公寓,要求顶点C在地块的对角线MN上,B,D分别在边AM,AN上,假设AB长度为x米.
某建筑工地在一块唱AM=30米,宽AN=20米的矩形地块AMPN上施工,规划建设占地如图中矩形ABCD的学生公寓,要求顶点C在地块的对角线MN上,B,D分别在边AM,AN上,假设AB长度为x米.(1)要是矩形学生公寓ABCD的面积不小于144平方米,AB的长度应在什么范围?
(2)长度AB和宽度AD分别为多少米是矩形学生公寓ABCD的面积最大?最大值是多少平方米?
分析 (1)首先利用三角形的相似性,求得边AD与边AB的长度关系,建立三角形面积函数模型,再由s≥144,得出边AB的长度范围;
(2)由二次函数配方求最值求得.
解答 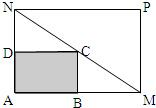 解:(1)依题意设AD=t,则$\frac{20-t}{20}$=$\frac{x}{30}$,
解:(1)依题意设AD=t,则$\frac{20-t}{20}$=$\frac{x}{30}$,
∴t=20-$\frac{2}{3}$x,
所以s=(20-$\frac{2}{3}$x)x,
又∵s≥144,
∴x2-30x+216≤0,解得12≤x≤18,
要使公寓ABCD的面积不小于144平方米,
即12≤x≤18,即AB的长度应在[12,18]内;
(2)s=(20-$\frac{2}{3}$x)x=-$\frac{2}{3}$(x-15)2+150,
当x=15时,t=20-10=10,s取得最大值150.
答:AB=15米,AD=10米时,公寓ABCD的面积最大,最大值是150平方米.
点评 本题主要考查二次函数的最值的求法和二次不等式的解法,考查运算能力,属于中档题.

练习册系列答案
相关题目
5.集合A={-1,0,1},B={x|x-1=0},则A∩B=( )
| A. | R | B. | {1} | C. | {0} | D. | {-1,0,1} |
6.若二项式($\sqrt{x}$+$\frac{1}{x}$)n(n>0且n∈N*)的展开式中含有常数项,那么指数n必为( )
| A. | 奇数 | B. | 偶数 | C. | 3的倍数 | D. | 6的倍数 |