题目内容
4.已知函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≤0}\\{{x}^{2}-2x+1,}&{x>0}\end{array}\right.$,若关于x的方程f[f(x)]=m恰有5个不同的实数解,则m的取值范围是( )| A. | m<0 | B. | 0<m<1 | C. | m=1 | D. | m>1 |
分析 作函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≤0}\\{{x}^{2}-2x+1,}&{x>0}\end{array}\right.$的图象,从而利用数形结合的方法求解即可.
解答 解:作函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≤0}\\{{x}^{2}-2x+1,}&{x>0}\end{array}\right.$的图象如下,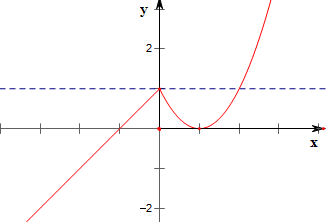
结合图象可知,当m<0时,f(x)=m有且只有一个解,
故方程f[f(x)]=m至多有三个解,故排除A;
当0<m<1时,f(x)=m有且只有三个解,
且分别在区间(-1,0),(0,1),(1,2)内,
故方程f[f(x)]=m有且只有5个解,
故选B.
点评 本题考查了方程的根与函数的零点的关系应用及数形结合的思想应用.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
15.设x,y满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-1≥0}\\{x≤3}\end{array}\right.$,则z=1+2x-3y的最小值是( )
| A. | -6 | B. | -5 | C. | -4 | D. | -2 |
9.下列函数中,值域为(0,+∞)的函数是( )
| A. | y=3${\;}^{\frac{2}{x}}$ | B. | y=$\sqrt{{2}^{x}-1}$ | C. | y=$\sqrt{{2}^{x}+1}$ | D. | y=($\frac{1}{2}$)2-x |
16.化简:$\frac{1}{lo{g}_{3}x}+\frac{1}{lo{g}_{4}x}+\frac{1}{lo{g}_{5}x}$=( )
| A. | $\frac{1}{lo{g}_{60}x}$ | B. | $\frac{1}{lo{g}_{3}x•lo{g}_{4}x•lo{g}_{5}x}$ | ||
| C. | $\frac{1}{lo{g}_{x}60}$ | D. | $\frac{12}{lo{g}_{3}x+lo{g}_{4}x+lo{g}_{5}x}$ |
 某建筑工地在一块唱AM=30米,宽AN=20米的矩形地块AMPN上施工,规划建设占地如图中矩形ABCD的学生公寓,要求顶点C在地块的对角线MN上,B,D分别在边AM,AN上,假设AB长度为x米.
某建筑工地在一块唱AM=30米,宽AN=20米的矩形地块AMPN上施工,规划建设占地如图中矩形ABCD的学生公寓,要求顶点C在地块的对角线MN上,B,D分别在边AM,AN上,假设AB长度为x米.