题目内容
若数列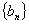 满足:对于
满足:对于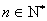 ,都有
,都有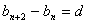 (常数),则称数列
(常数),则称数列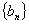 是公差为
是公差为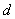 的准等差数列.如:若
的准等差数列.如:若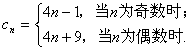 则
则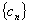 是公差为
是公差为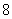 的准等差数列.
的准等差数列.
(1)求上述准等差数列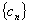 的前
的前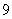 项的和
项的和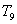 ;
;
(2)设数列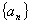 满足:
满足: ,对于
,对于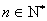 ,都有
,都有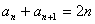 .求证:
.求证: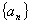 为准等差数列,并求其通项公式;
为准等差数列,并求其通项公式;
(3)设(2)中的数列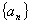 的前
的前 项和为
项和为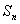 ,试研究:是否存在实数
,试研究:是否存在实数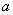 ,使得数列
,使得数列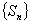 有连续的两项都等于
有连续的两项都等于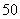 .若存在,请求出
.若存在,请求出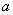 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解:(1)
(2) (
(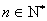 )①
)①
 ②
②
②-①得 (
(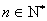 ).
).
所以,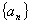 为公差为2的准等差数列.
为公差为2的准等差数列.
当 为偶数时,
为偶数时, ,
,
当 为奇数时,解法一:
为奇数时,解法一: ;
;
解法二: ;
;
解法三:先求 为奇数时的
为奇数时的 ,再用①求
,再用①求 为偶数时的
为偶数时的 同样给分.
同样给分.

(3)解一:
当 为偶数时,
为偶数时, ;
;
当 为奇数时,
为奇数时,
 .
.
当 为偶数时,
为偶数时, ,得
,得 .
.
由题意,有 ;
;
或 . 所以,
. 所以, .
.
解二:当 为偶数时,
为偶数时, ,
, 
当 为奇数时,
为奇数时,
 .
.
以下与解法一相同.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 的定义域是集合A,
的定义域是集合A, 定义域是集合B。
定义域是集合B。 ,求实数
,求实数 的取值范围。
的取值范围。 
 ,则
,则 的值为( )
的值为( ) .
. 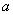
 .
. 
 .
.  中较小的数
中较小的数  .
.  为单位向量,且
为单位向量,且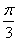 ,若
,若 ,
, ,则向量
,则向量 在
在 方向上的投影为___________.
方向上的投影为___________. 、
、 、
、 是空间三条不同的直线,下列命题中正确的是( )
是空间三条不同的直线,下列命题中正确的是( )  如果
如果 ,
, .则
.则 .
.  如果
如果 ,
, 如果
如果 .则
.则 如果
如果 >
>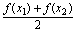 恒成立的函数的个数是 ( )
恒成立的函数的个数是 ( ) a20=78,则此数列前20项和等于 ( )
a20=78,则此数列前20项和等于 ( ) 在
在 上是单调减函数,则实数
上是单调减函数,则实数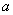 的取值范围是
的取值范围是