题目内容
曲线y2=x在点P(1,1)处切线方程 .
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:根据P点的坐标得到P为第一象限的点,所以得到y=
,然后求出y′,把x=1代入y′求得切线的斜率,根据P点坐标和斜率写出切线的方程即可.
| x |
解答:
解:因为P点在第一象限,由曲线y2=x即y=
,所以y′=
,
把x=1代入y′求得切线的斜率k=
,
则曲线在P点的切线方程为y-1=
(x-1),即x-2y+1=0
故答案为:x-2y+1=0.
| x |
| 1 | ||
2
|
把x=1代入y′求得切线的斜率k=
| 1 |
| 2 |
则曲线在P点的切线方程为y-1=
| 1 |
| 2 |
故答案为:x-2y+1=0.
点评:此题考查学生会利用导数研究曲线上某点的切线方程,是一道综合题.学生在解决此类问题一定要分清“在某点处的切线”,还是“过某点的切线”;同时解决“过某点的切线”问题,一般是设出切点坐标解决.

练习册系列答案
相关题目
过原点的直线l的倾斜角取值范围为[60°,135°]时,其斜率的取值范围为( )
A、[-1,
| ||||
B、(-∞,-1]∪[
| ||||
C、[1,
| ||||
D、[-1,
|
下列函数:①y=xsinx,②y=xcosx,③y=x|cosx|,④y=x2x的图象(部分)如图(但顺序被打乱):则从左到右的各图象依次对应的函数序号是( )
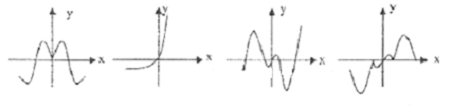

| A、①④②③ | B、①④③② |
| C、④①②③ | D、③④②① |
 如图是2011年在某市举行的红歌大赛上,七位评委为某歌手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为
如图是2011年在某市举行的红歌大赛上,七位评委为某歌手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为