题目内容
5.设f(x)是R上的可导函数,且f′(x)≥-f(x),f(0)=1,f(2)=$\frac{1}{{e}^{2}}$.则f(1)的值为$\frac{1}{e}$.分析 根据条件构造函数g(x)=f(x)ex,求函数的导数,研究函数的单调性即可得到结论.
解答 解:设g(x)=f(x)ex,
则g′(x)=f′(x)ex+f(x)ex=ex(f′(x)+f(x)),
∵f′(x)≥-f(x),∴f′(x)+f(x)≥0,
则g′(x)≥0,
则函数g(x)为单调递增函数或常数函数,
∵f(0)=1,f(2)=$\frac{1}{{e}^{2}}$.
∴g(0)=f(0)e0=1,
g(2)=f(2)e2=1,
则g(0)=g(2)=1,
∴函数g(x)是常数函数,
则g(x)=1,即g(1)=f(1)e=1,
则f(1)=$\frac{1}{e}$,
故答案为:$\frac{1}{e}$
点评 本题主要考查函数值的计算,根据条件构造函数,求函数的导数研究函数单调性的性质是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.若全集U={0,1,2,3,4,5,6},A={1,3},B={3,5},则∁U(A∪B)=( )
| A. | {2,4} | B. | {2,4,6} | C. | {0,2,4} | D. | {0,2,4,6} |
14.曲线的切线方程与直线6x-3y+1=0相互垂直,其中x的取值为非正数且曲线的方程为f(x)=2x3+x2-x(x2-1),则曲线的切线方程为( )
| A. | 2x+y+1=0 | B. | 2x+y-1=0 | C. | 2x-y-1=0 | D. | 2x-y+1=0 |
15.已知a=sin80°,$b={(\frac{1}{2})^{-1}}$,$c={log_{\frac{1}{2}}}3$,则( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
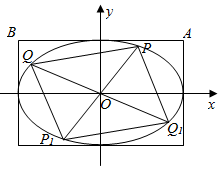 已知椭圆C的中心在原点,对称轴为坐标轴,左焦点为F1(-1,0),离心率为$\frac{1}{2}$.
已知椭圆C的中心在原点,对称轴为坐标轴,左焦点为F1(-1,0),离心率为$\frac{1}{2}$.