题目内容
6.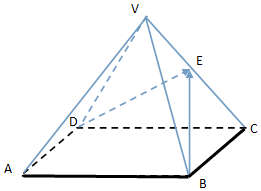 如图,在正四棱锥V-ABCD中,E为VC的中点,正四棱锥的底面边长为2a,高为h
如图,在正四棱锥V-ABCD中,E为VC的中点,正四棱锥的底面边长为2a,高为h(1)求cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>
(2)当∠BED是二面角B-VC-D的平面角时,求∠BED的正弦值.
分析 由题意建立空间直角坐标系.
(1)由已知求出B、C、V、E的坐标,可得$\overrightarrow{BE}、\overrightarrow{DE}$的坐标,然后利用数量积求夹角公式可得cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>;
(2)由∠BED是二面角B-VC-D的平面角,得DE⊥CV,由$\overrightarrow{DE}•\overrightarrow{CV}=0$,得h2=2a2,可得cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>,再由平方关系求得∠BED的正弦值.
解答 解:以正四棱锥V-ABCD的底面中心O为坐标原点建立如图所示空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,
(1)由已知可得B(a,a,0),C(-a,a,0),V(0,0,h),E($-\frac{a}{2}$,$\frac{a}{2}$,$\frac{h}{2}$),
∴$\overrightarrow{BE}$=($-\frac{3}{2}a,-\frac{a}{2},\frac{h}{2}$),$\overrightarrow{DE}=(\frac{a}{2},\frac{3a}{2},\frac{h}{2})$,
故cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=$\frac{{h}^{2}-6{a}^{2}}{{h}^{2}+10{a}^{2}}$;
(2)当∠BED是二面角B-VC-D的平面角时,
有DE⊥CV,由$\overrightarrow{DE}•\overrightarrow{CV}=0$,得$\frac{{a}^{2}}{2}-\frac{3{a}^{2}}{2}+\frac{{h}^{2}}{2}=0$,
即h2=2a2,于是由(1)得cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=$\frac{{h}^{2}-6{a}^{2}}{{h}^{2}+10{a}^{2}}$=$\frac{-4{a}^{2}}{12{a}^{2}}=-\frac{1}{3}$,
∴sin$∠BED=\sqrt{1-(-\frac{1}{3})^{2}}=\frac{2\sqrt{2}}{3}$.
点评 本题考查二面角的平面角及其求法,考查空间想象能力和思维能力,训练了利用空间向量求解二面角的平面角,是中档题.

| A. | (-1,0)、(0,1) | B. | (-∞,0)、(1,+∞) | C. | (0,3) | D. | (0,1) |
 如图,在直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M,N分别是棱CC1,BC的中点,点P在直线A1B1上.
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M,N分别是棱CC1,BC的中点,点P在直线A1B1上. 如图所示,在Rt△ABC中,AC⊥BC,有AC2+BC2=AB2;类比猜想:直角四面体P-ABC(即PA⊥PB,PB⊥PC,PC⊥PA)的四个面的面积关系,证明你的猜想.
如图所示,在Rt△ABC中,AC⊥BC,有AC2+BC2=AB2;类比猜想:直角四面体P-ABC(即PA⊥PB,PB⊥PC,PC⊥PA)的四个面的面积关系,证明你的猜想.