题目内容
11.数列{an}满足a1=1,且对于任意的n∈N*都满足${a_{n+1}}=\frac{a_n}{{3{a_n}+1}}$,则数列{anan+1}的前10项和为$\frac{10}{31}$.分析 对于任意的n∈N*都满足${a}_{n+1}=\frac{{a}_{n}}{3{a}_{n}+1}$,两边取倒数可得:$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}}$+3,即$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=3,再利用等差数列的通项公式、裂项求和方法即可得出.
解答 解:对于任意的n∈N*都满足${a}_{n+1}=\frac{{a}_{n}}{3{a}_{n}+1}$,
两边取倒数可得:$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}}$+3,即$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=3,
∴数列$\{\frac{1}{{a}_{n}}\}$为等差数列,公差为3,首项为1.
∴$\frac{1}{{a}_{n}}$=1+3(n-1)=3n-2.
∴an=$\frac{1}{3n-2}$.
∴anan+1=$\frac{1}{(3n-2)(3n+1)}$=$\frac{1}{3}(\frac{1}{3n-2}-\frac{1}{3n+1})$.
则数列{anan+1}的前n项和=$\frac{1}{3}[(1-\frac{1}{4})+(\frac{1}{4}-\frac{1}{7})$+…+$(\frac{1}{3n-2}-\frac{1}{3n+1})]$
=$\frac{1}{3}(1-\frac{1}{3n+1})$=$\frac{n}{3n+1}$.
∴则数列{anan+1}的前10项和=$\frac{10}{31}$.
故答案为:$\frac{10}{31}$.
点评 本题考查了数列递推关系、等差数列的通项公式及其性质、裂项求和方法,考查了推理能力与计算能力,属于中档题.

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | {-1,0,1} | B. | {0,1} | C. | (-1,1) | D. | (-1,3) |
| A. | 第一枚6点,第二枚2点 | B. | 第一枚5点,第二枚1点 | ||
| C. | 第一枚1点,第二枚6点 | D. | 第一枚6点,第二枚1点 |

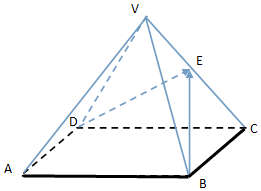 如图,在正四棱锥V-ABCD中,E为VC的中点,正四棱锥的底面边长为2a,高为h
如图,在正四棱锥V-ABCD中,E为VC的中点,正四棱锥的底面边长为2a,高为h 如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且3bsinA=c,D为AC边上一点.
如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且3bsinA=c,D为AC边上一点.