题目内容
18.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-6≤0}\\{x-y-1≤0}\\{x-1≤0}\end{array}\right.$,若z=ax+2y仅在点$({\frac{7}{3},\frac{4}{3}})$处取得最大值,则a的值可以为( )| A. | -8 | B. | -4 | C. | 4 | D. | 8 |
分析 画出约束条件的可行域,求出顶点坐标,利用z=ax+2y仅在点$({\frac{7}{3},\frac{4}{3}})$处取得最大值,利用斜率关系求解即可.
解答  解:如图所示,约束条件$\left\{\begin{array}{l}{2x+y-6≤0}\\{x-y-1≤0}\\{x-1≤0}\end{array}\right.$,所表示的区域为图中阴影部分:其中A(1,0),B$({\frac{7}{3},\frac{4}{3}})$,C(1,4),
解:如图所示,约束条件$\left\{\begin{array}{l}{2x+y-6≤0}\\{x-y-1≤0}\\{x-1≤0}\end{array}\right.$,所表示的区域为图中阴影部分:其中A(1,0),B$({\frac{7}{3},\frac{4}{3}})$,C(1,4),
依题意z=ax+2y仅在点$({\frac{7}{3},\frac{4}{3}})$处取得最大值,可得-$\frac{a}{2}$=-2,即,a=4.
故选:C.
点评 本题考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
7.命题:“?x∈(-∞,0),x3+x≥0”的否定是( )
| A. | ?x0∈(-∞,0),x03+x0<0 | B. | ?x∈(-∞,0),x3+x≥0 | ||
| C. | ?x0∈[0,+∞),x3+x<0 | D. | ?x0∈[0,+∞),x03+x0≥0 |
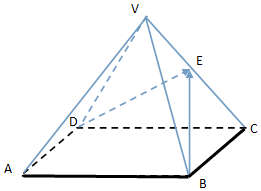 如图,在正四棱锥V-ABCD中,E为VC的中点,正四棱锥的底面边长为2a,高为h
如图,在正四棱锥V-ABCD中,E为VC的中点,正四棱锥的底面边长为2a,高为h 如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且3bsinA=c,D为AC边上一点.
如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且3bsinA=c,D为AC边上一点.